Screen S is illuminated by two point sources A and B. Another source C sends a parallel beam of light towards point P on the screen (see figure). Line AP is normal to the screen and the lines AP, BP and CP are in one plane. The distance AP, BP and CP are 3m, 1.5m and 1.5m respectively. The radiant powers of sources A and B are 90was and 180was respectively. The beam from C is of intensity 20wasm2. Calculate the intensity at P on the screen.
The correct Answer is:A, C

The total intensity at point P will be =IA+IB+IC
IA=(illuminationpower)×cosθ4πr2=90×cosθ4π×32=104π wasm2
IB=180×cos60degree4π×(1.5)2=10πwa/m2
IC=20cos60degree=10
∵Ip=104π+10π+10=13.9Wm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
A photoelectric cell is illuminated by a point source of light 1m away . When the source is shifted to 2m then
ANumber of electrons emitted is half the initial numberBEach emitted electron carries half the initial energyCNumber of electrons emitted is a quarter of the initial numberDEach emitted electron carries one quarter of the initial energyTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesIf the distance between a point source and screen is doubled, then intensity of light on the screen will become
AFour timesBDoubleCHalfDOne-fourth
In the given figure ,secants AP and CP intersect in point P. If AP=12,PB=5,CP=20, then DP=
View SolutionTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View SolutionThe optical path difference at a point on the screen which is equidistant from two sources is
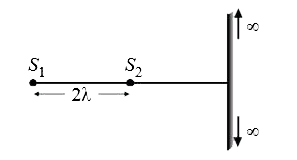
View SolutionThere are two sources kept at distances 2λ. A large screen is perpendicular to line joining the sources. Number of maximas on the screen in this case is (λ=wavelength of light)
View SolutionIn a Fresnel's biprims experiment fringes widht 0.05 mm are observed on a screen at a distance of 1.5 m from the source. When a convex lens is placed between the source and the screen, are 0.04 mm and 0.1 mm resepectively. The wavelenght of light used is s
View Solution