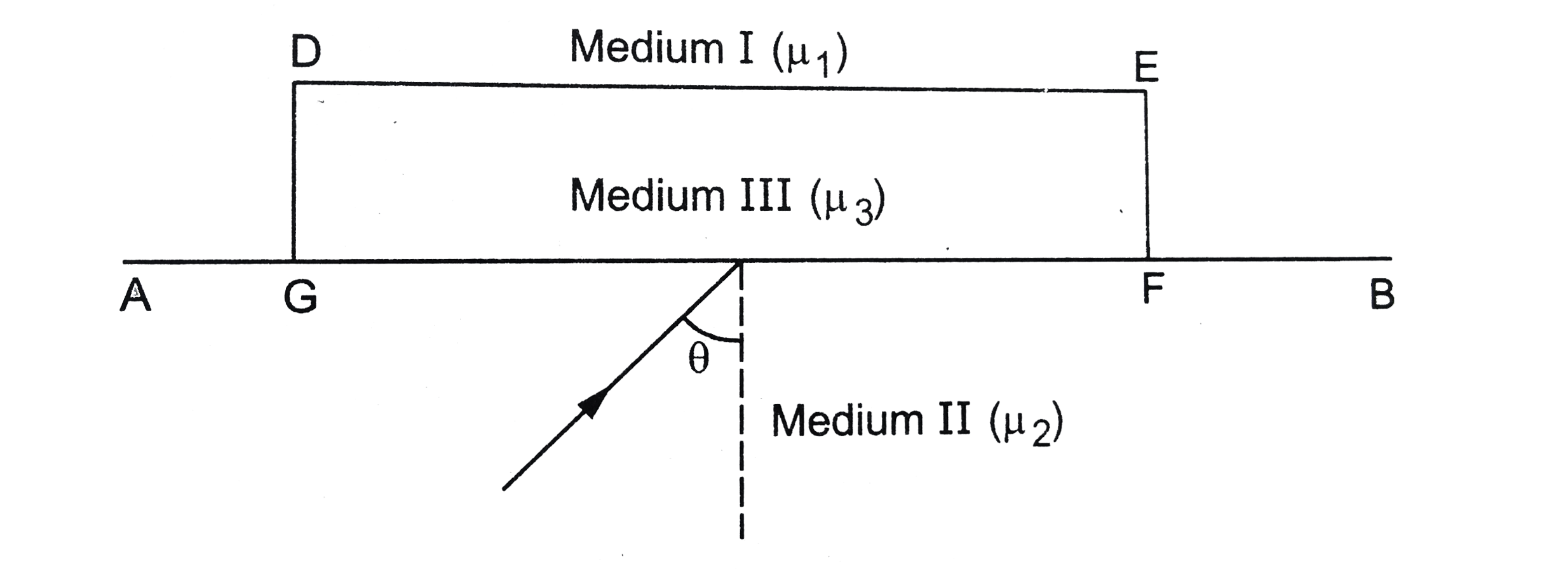
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

The correct Answer is:A
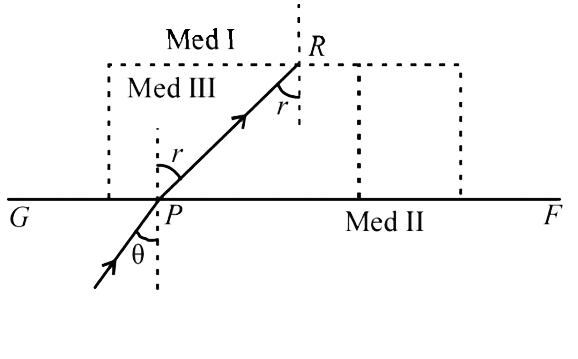
KEY CONCEPT: For total internal reflection, the condition are
The object should be in the denser medium.
The angle of incidence should be greater than the critical angle
Case (i): When n3<n1
Obviously n3<n2 and the angle θ is greater than the critical angle required for the ray passing from medium II to medium III. Therefore total internal reflection will also take place when a ray strikes with the same angle at the interface of medium II and medium III.
Case (ii): n3>n(1) but n3<n2
The ray will get refracted in medium III as the angle θ will now be less than the critical angle required for medium II
sinθsinr=n3n2..(Applying Snell's law at P)
∵ sinr=n2n3sinθ
As n2>n3 So, r>θ
When the refracted ray PR meets the boundary DE, it is travelling from a denser medium to a rarer medium. Therefore the ray will be totally internally reflected at DE if its angle of incidence r is more than the critical angle for med III and I.
sinin=n1n3
Since, sinr>n1n3⇒sinr>sini)⇒r>i)
Therefore ray PR will be totally internal reflected along RQ. On reaching Q, the ray will be refracted in med II. Thus, the ray will ultimately be reflected back in medium II.
Topper's Solved these Questions
Similar Questions
Monochramatic light is incident on the pane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
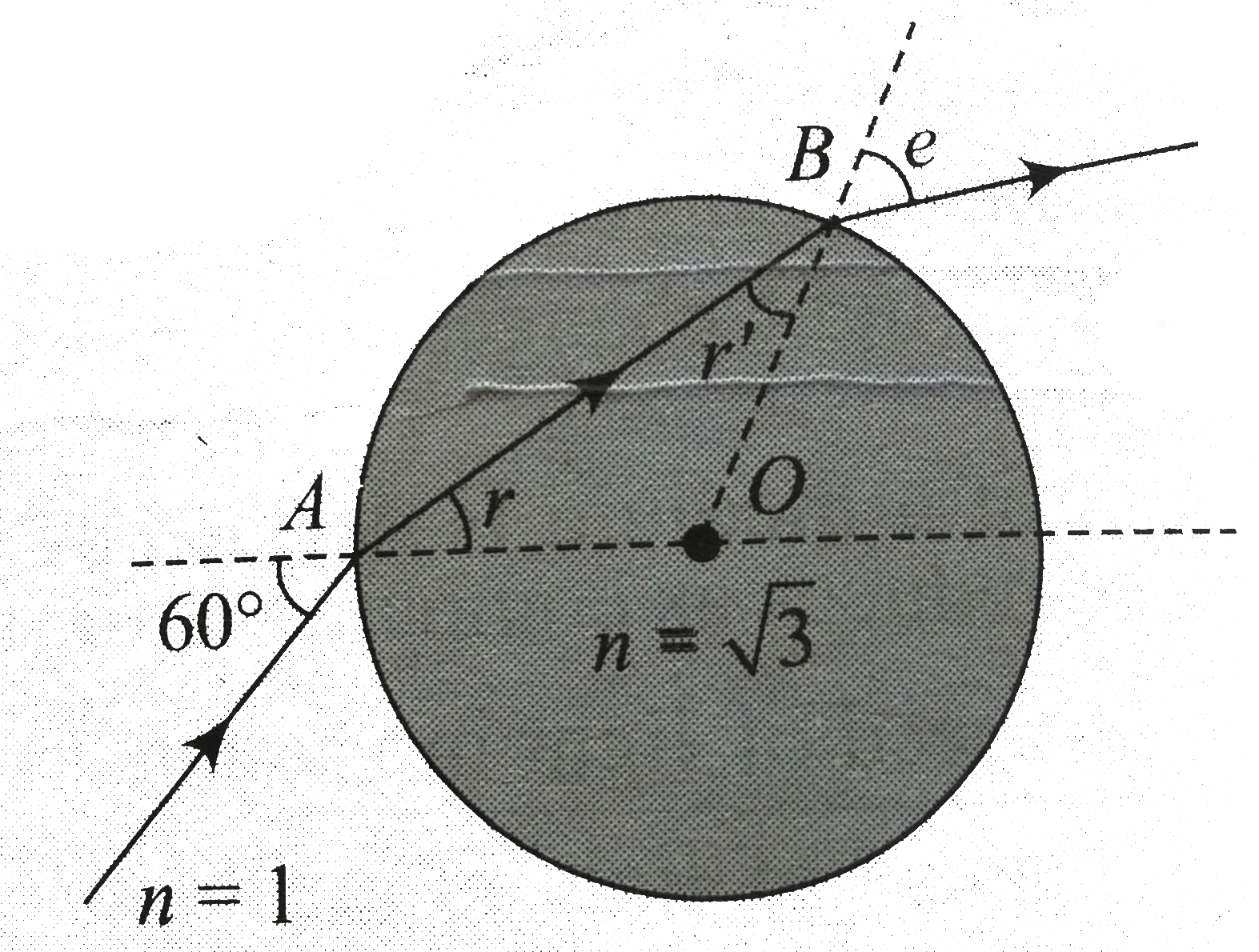
View Solution
Knowledge Check

A ray is incident on interface of two media at critical angle as shown in the figure.Aif μ1 and μ2 both are increased by same amount the ray will suffer total internal reflection.Bif μ1 and μ2 both are increased by same amount the ray will suffer refraction and angle of refraction will be less then 90∘Cif μ1 and μ2 both are doubled ray will suffer total internal reflection.Dif μ1 ad μ2 both are doulbed ray will suffer refraction and angle of refraction will be less te 90∘In total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
A180∘B0∘CEqual to angle of incidenceD90∘Two optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
A(x−y)xB(x+y)xCxy−xDyx
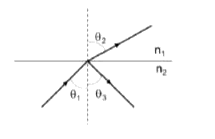
A monochromatic beam of light is incident at the interface of two materials of refractive index n1 and n2 as shown . If n1>n2 and θC is the critical angle then which of the following statements is NOT true ?
View SolutionTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
View SolutionFor total internal reflection to take place, the angle of incidence I and the refractive index μ of the medium must satisfy the inequality
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionIf a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
View Solution
