Seven capacitors each of capacitance are to be connected in a configuration to obtain an effective capacitance of . Which of the combination (s) shown in figure will achieve the desired result?
(a) 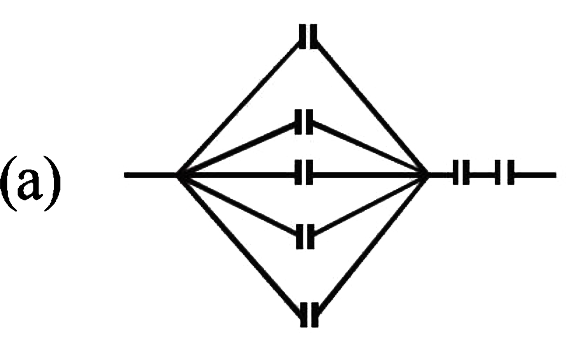
(b) 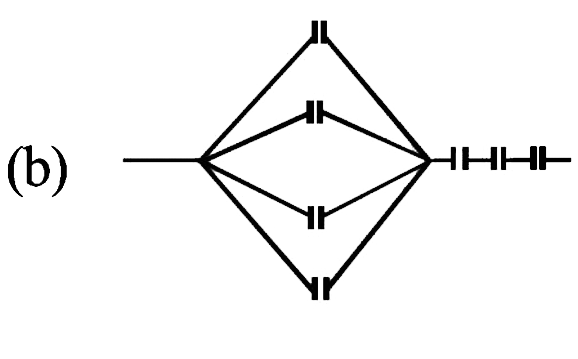
(c) 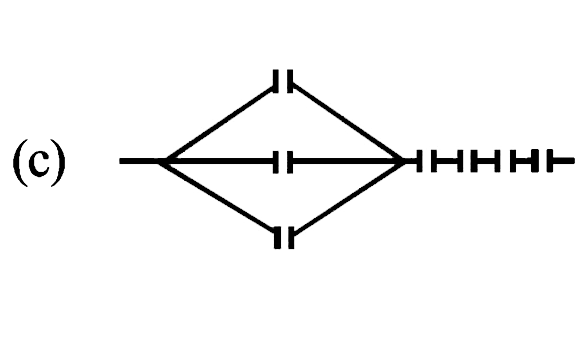
(d) 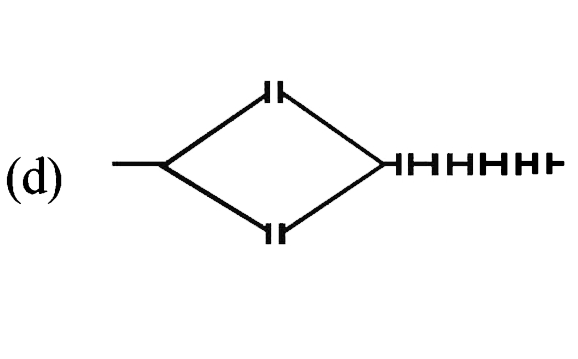
The correct Answer is:A
To solve the problem of finding the correct combination of capacitors to achieve an effective capacitance of 1011μF using seven capacitors each of capacitance 2μF, we will analyze the configurations provided in the options.
1. Identify the Configuration:
We need to analyze the first configuration presented. It consists of several capacitors connected in parallel and then in series.
2. Calculate the Capacitance of the Parallel Section:
In the first configuration, there are five capacitors connected in parallel. The formula for the total capacitance Cp of capacitors in parallel is:
Cp=C1+C2+C3+C4+C5
Since each capacitor has a capacitance of 2μF:
Cp=2+2+2+2+2=10μF
3. Calculate the Capacitance of the Series Section:
The total capacitance of the parallel section Cp is then connected in series with two other capacitors, each of 2μF. The formula for the total capacitance Cs of capacitors in series is:
1Cs=1Cp+1C6+1C7
Substituting the values:
1Cs=110+12+12
To simplify, we can convert 12 to have a common denominator of 10:
1Cs=110+510+510=1+5+510=1110
4. Find the Effective Capacitance:
Now, we can find Cs:
Cs=1011μF
5. Conclusion:
The configuration analyzed indeed gives us the desired effective capacitance of 1011μF. Therefore, the first configuration is the correct option.
We need to analyze the first configuration presented. It consists of several capacitors connected in parallel and then in series.
In the first configuration, there are five capacitors connected in parallel. The formula for the total capacitance Cp of capacitors in parallel is:
Cp=C1+C2+C3+C4+C5
Since each capacitor has a capacitance of 2μF:
Cp=2+2+2+2+2=10μF
The total capacitance of the parallel section Cp is then connected in series with two other capacitors, each of 2μF. The formula for the total capacitance Cs of capacitors in series is:
1Cs=1Cp+1C6+1C7
Substituting the values:
1Cs=110+12+12
To simplify, we can convert 12 to have a common denominator of 10:
1Cs=110+510+510=1+5+510=1110
Now, we can find Cs:
Cs=1011μF
The configuration analyzed indeed gives us the desired effective capacitance of 1011μF. Therefore, the first configuration is the correct option.
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions2videos
ELECTROSTATICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced107videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer1videos
MODERN PHYSICS
Similar Questions
Seven capacitors, each a of a cpacitance 2μF, are to be connected in a configuration to obatin an effective capacitance of (1613)μF. Which of the combinations, shown in figure below, will achieve the desired value ?
View SolutionFive capacitors each of capacitance 20μF are joined as shown in the figure. The equivalent capacitance between A and C is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
A B
B C
C D
D
- Question 2 - Select One
Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
AConnecting them in parallelBConnecting two in series and one in parallelCConnecting two in parallel and one in seriesDConnecting all of them in series - Question 3 - Select One
Six capacitors each of capacitance of 2μF are connected as shown in the figure. The effective capacitance between A and B is:
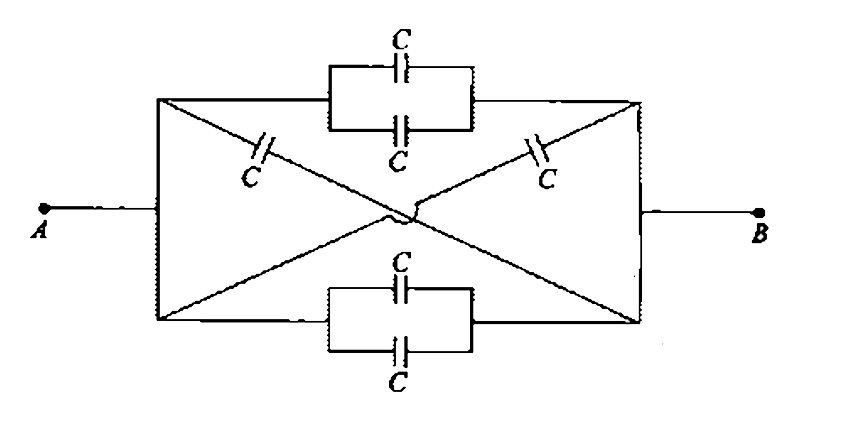 A12μFB8/3μFC3μFD6μF
A12μFB8/3μFC3μFD6μF
Some capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
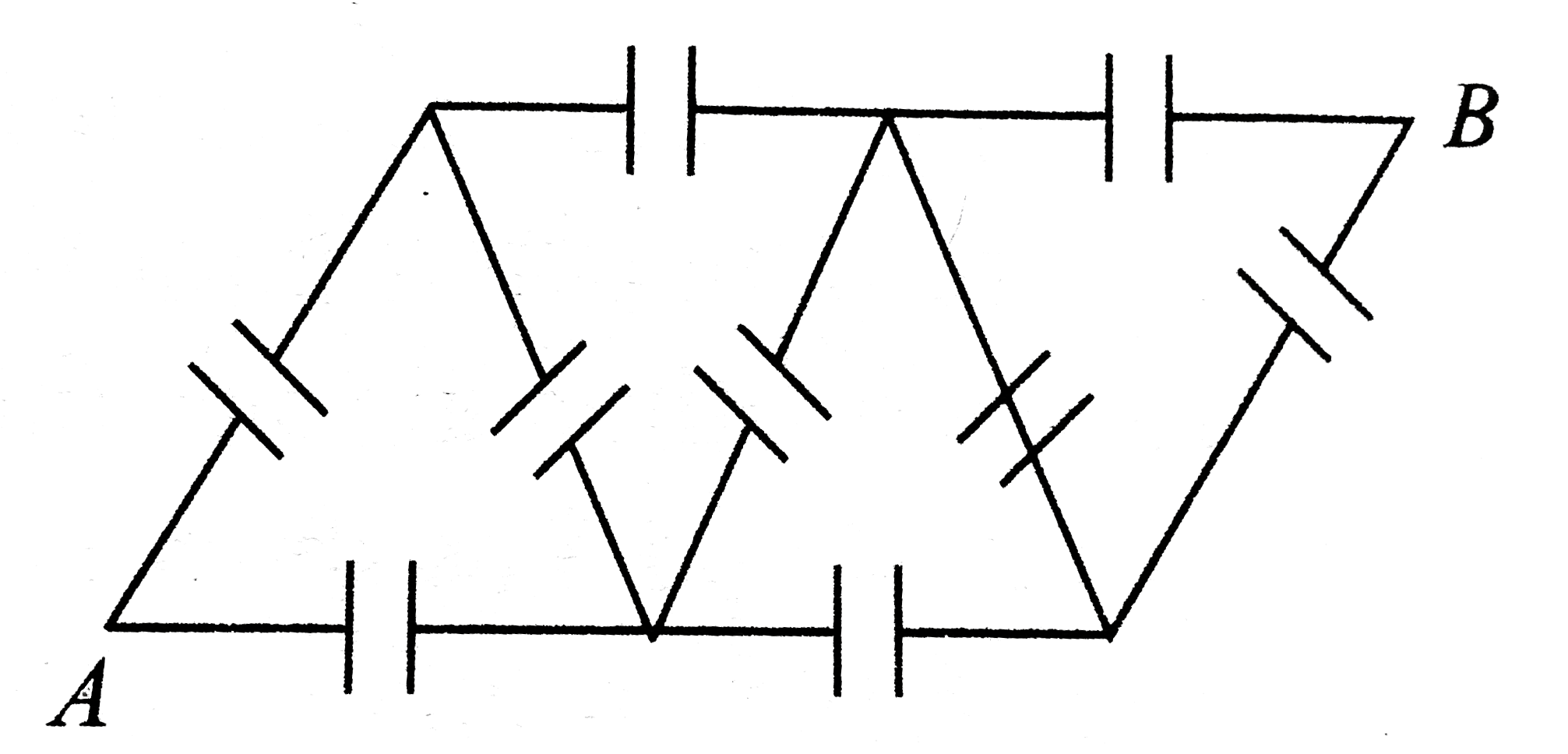 .View Solution
.View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then their maximum and minimum capacitances will be
View SolutionEight capacitors , each of capacitance 2μF are conneted as shown in the figure . The effective capacitance between point A and B is
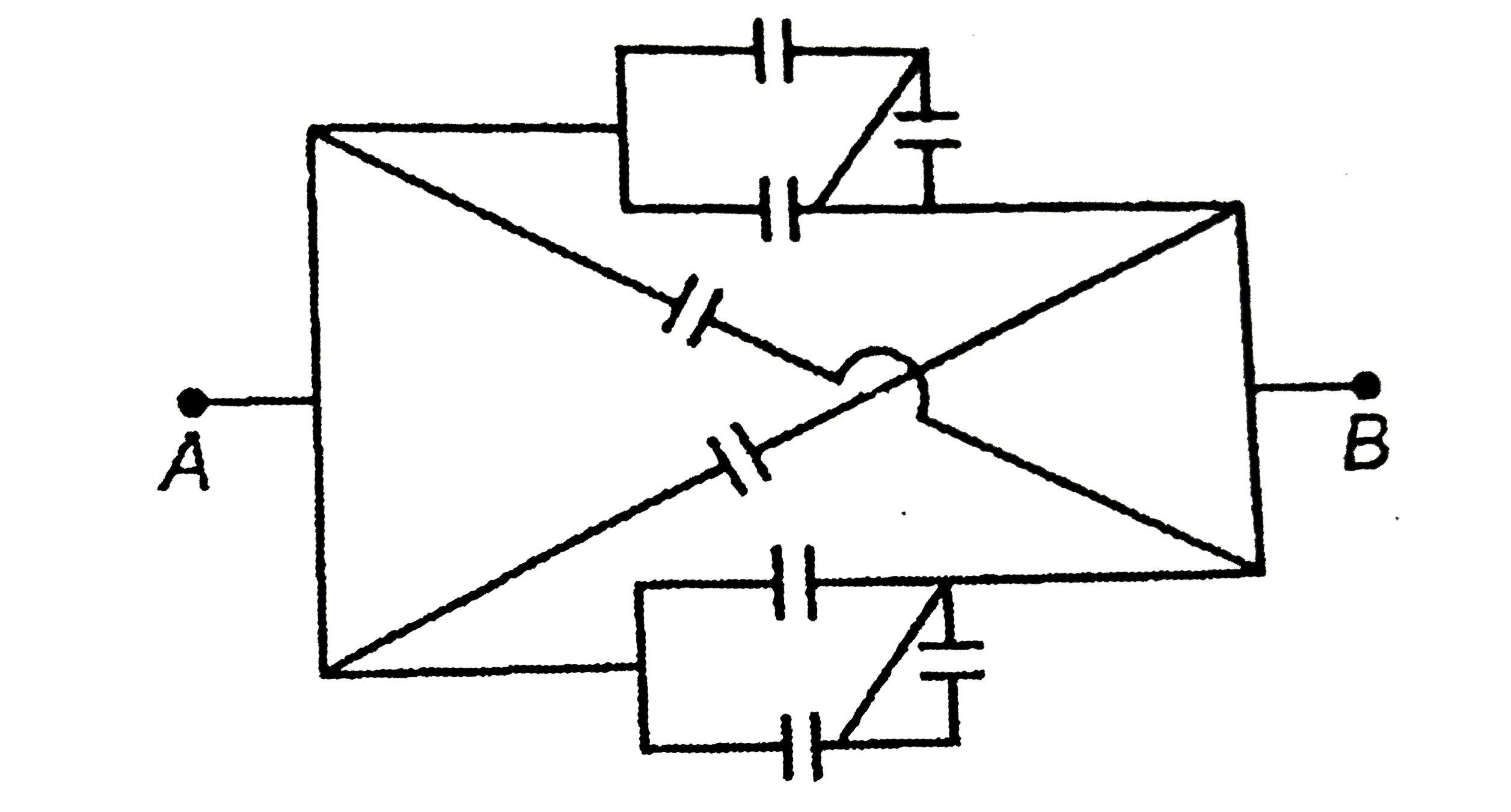 View Solution
View SolutionSeven capacitors each of capacity 2μF are to be so connected to have a total capacity (10/1)μF. Which will be the necessary figure as shown?
View Solution

