Three capacitors of capacitance 3μF are connected in a circuit. Then their maximum and minimum capacitances will be
9μF,1μF
8μF,2μF
9μF,0μF
3μF,2μF
The correct Answer is:A
To solve the problem of finding the maximum and minimum capacitance of three capacitors, each with a capacitance of 3μF, we will analyze both the parallel and series configurations.
1. Understanding Capacitor Configurations:
- Capacitors can be connected in two main configurations: parallel and series.
- In a parallel connection, the total capacitance is the sum of the individual capacitances.
- In a series connection, the total capacitance is given by the reciprocal of the sum of the reciprocals of the individual capacitances.
2. Calculating Maximum Capacitance:
- For maximum capacitance, we connect the capacitors in parallel.
- The formula for total capacitance Cmax in parallel is:
Cmax=C1+C2+C3
- Given that each capacitor has a capacitance of 3μF:
Cmax=3μF+3μF+3μF=9μF
3. Calculating Minimum Capacitance:
- For minimum capacitance, we connect the capacitors in series.
- The formula for total capacitance Cmin in series is:
1Cmin=1C1+1C2+1C3
- Since all capacitors are the same, we can simplify this to:
1Cmin=3Cwhere C=3μF
- Therefore:
1Cmin=33μF=1μF
- Inverting this gives:
Cmin=1μF
4. Final Results:
- The maximum capacitance when connected in parallel is 9μF.
- The minimum capacitance when connected in series is 1μF.
Summary:
- Maximum Capacitance: 9μF
- Minimum Capacitance: 1μF
---
- Capacitors can be connected in two main configurations: parallel and series.
- In a parallel connection, the total capacitance is the sum of the individual capacitances.
- In a series connection, the total capacitance is given by the reciprocal of the sum of the reciprocals of the individual capacitances.
- For maximum capacitance, we connect the capacitors in parallel.
- The formula for total capacitance Cmax in parallel is:
Cmax=C1+C2+C3
- Given that each capacitor has a capacitance of 3μF:
Cmax=3μF+3μF+3μF=9μF
- For minimum capacitance, we connect the capacitors in series.
- The formula for total capacitance Cmin in series is:
1Cmin=1C1+1C2+1C3
- Since all capacitors are the same, we can simplify this to:
1Cmin=3Cwhere C=3μF
- Therefore:
1Cmin=33μF=1μF
- Inverting this gives:
Cmin=1μF
- The maximum capacitance when connected in parallel is 9μF.
- The minimum capacitance when connected in series is 1μF.
- Maximum Capacitance: 9μF
- Minimum Capacitance: 1μF
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits52videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Problems Based On Mixed Concepts44videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor With Dielectric32videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Three capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
A9μF,1μFB8μF,2μFC9μF,0,μCD3μF,2μF - Question 2 - Select One
Three capacitors each of capacitance 1μF are connected in parallel. To this combination, a fourth capacitor capacitance 1μF is connected in series. The resultant capacitance of the system is
A4μFB2μFC43μFD34μF - Question 3 - Select One
In the figure, three capacitors each of capacitance 6pF are connected in series. The total capacitance of the combination will be
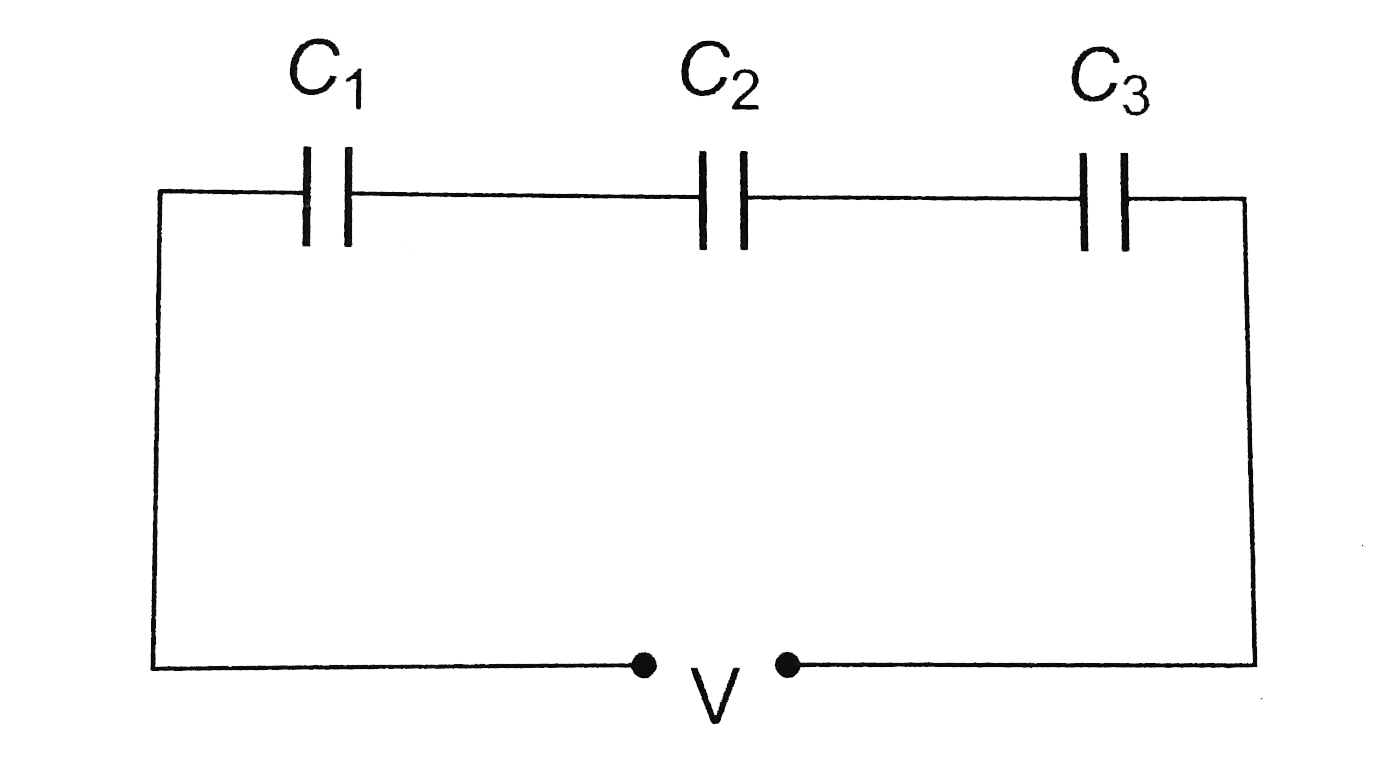 A9×10−12FB6×10−12FC3×10−12FD2×10−12F
A9×10−12FB6×10−12FC3×10−12FD2×10−12F
Some capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
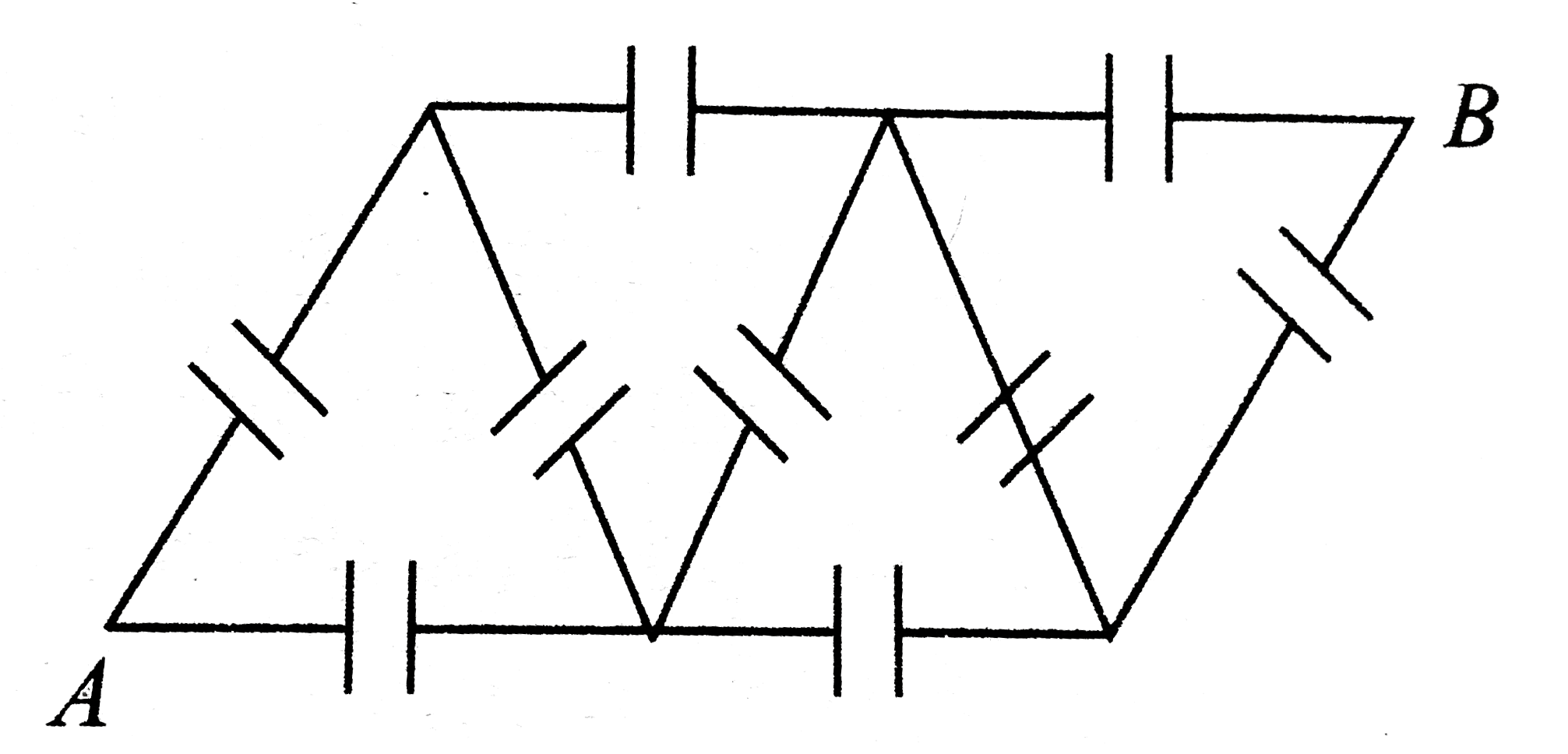 .View Solution
.View SolutionThree capacitors each of capacitance 1μF are connected in parallel.To this combination,a fourth capacitor of capacitance 1μFis connected in series.The resultant capacitance of the system
View SolutionThree capacitor of capacitance C(μF) are connected in parallel to which a capacitor of capacitance C is connected in series. Effective capacitance is 3.75. then capacity off each capacitor is
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
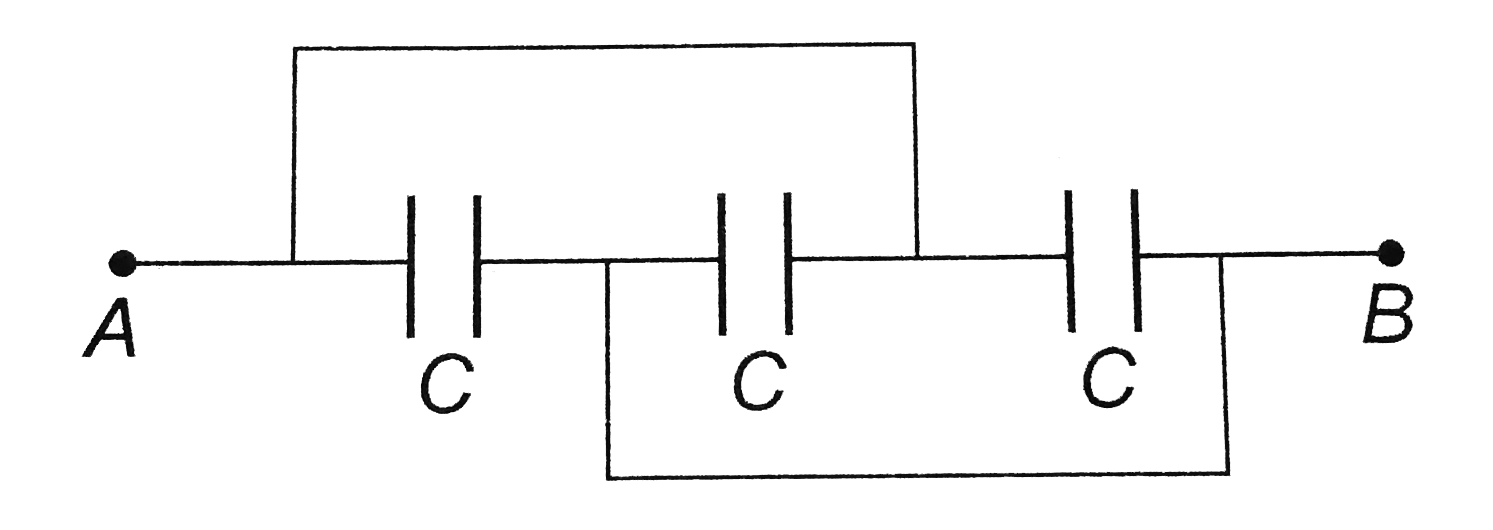 View Solution
View SolutionThree capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
View Solution

