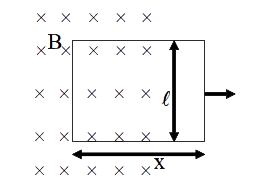
Show a rectangular loop MNOP being pulled out of a magnetic field with a uniform velocity v by applying an external force F. The length MN is equal to l and the total resistance of the loop is R. Find(a) the current in the loop,(b) the magnetic force on the loop, (c) the external force F needed to move it at constant velocity, (d) the power delivered by the external force and (e) the thermal power developed in the loop.
(a) The emf induced in the loop is due to the motion of the wire MN
The emf is ɛ=vBl with the positive end at N and the negative and at M
The current is I=(ɛ)(R)=vBIR in the clockwise direction (b) The magnetic force on the wire MN is →F1=i→LX→B
The magnitude is F1=ilB=vB2l2R and is opposite to the velocity
the forces on the parts of the wire NO and PM, lying in the fijled, cancle each other
The resultant magnetic force on the loop is, therfore, F1=Bl^2vR opposite ot the velocity
(c)To move the loop at a constant velocity, the resultant force on it should be zero
Thus, one should pull the loop with a force F=F1=vB2l2R
(d) The power delivered by the external force is P=FV=v2B2l2R (e) The thermal power developed is P=l2R=(vBIR)2R=v2B2l2R
We see that the power delivered by the external force is equal to the thermal power developed in the loop
this is consistent with the principle of conservation of energy
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Worked Out Examples29videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer13videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
A rectangular loop of resistance R, and sides l and X, is pulled out of a uniform magnetic field B with a for maintaining uniform velocity of withdrawal is __
ABl2vRBB2l2vRCB2l2v2RD0 - Question 2 - Select One or More
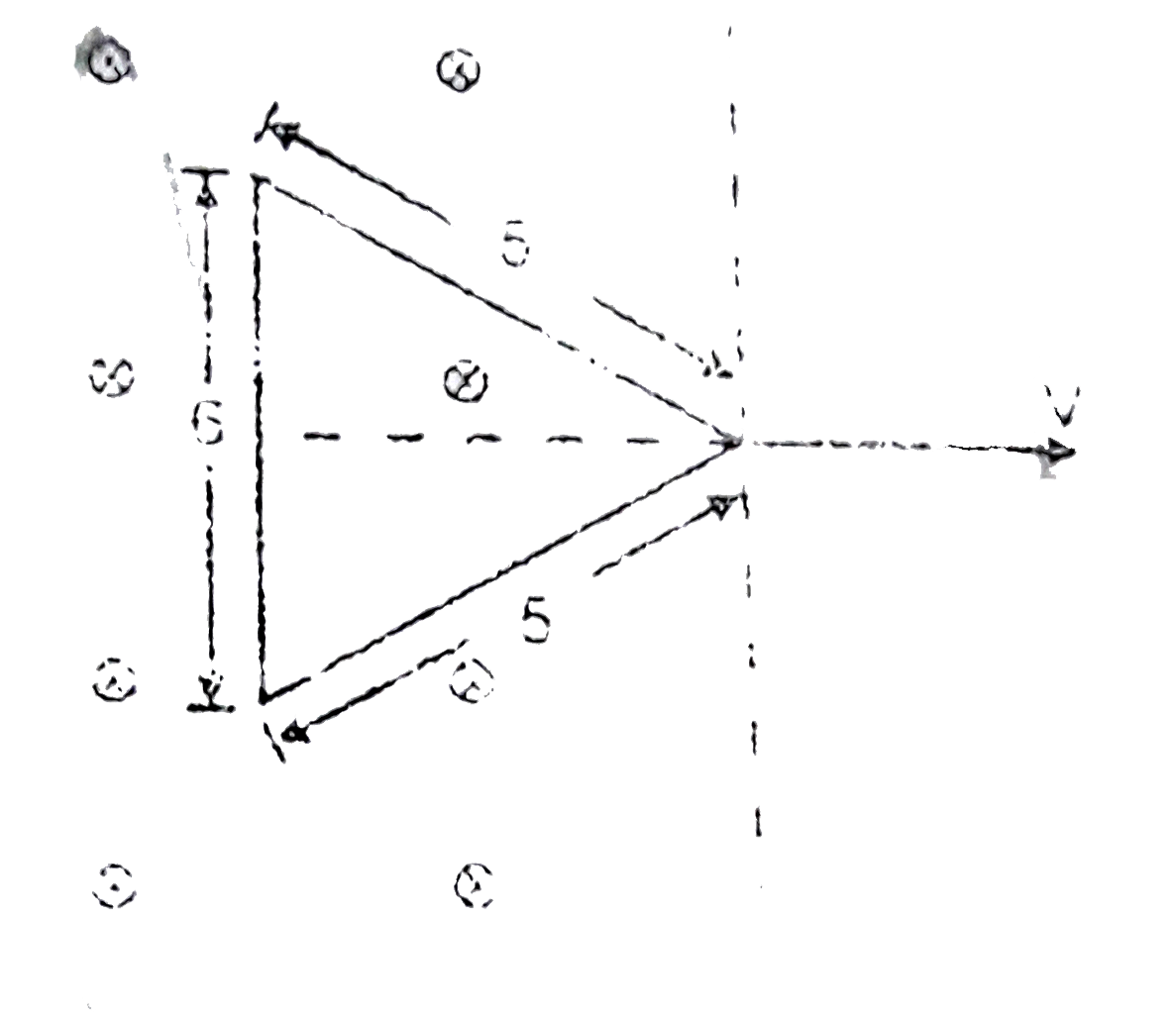
A triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be :
Apower produced in the loop increasing linearly with time till whole loop comes outBpower produced in the loop increases parabolically till whole loop comes outCCurrent in the loop increases linearly with time till whole loop comes outDpower produced in the loop will be constant with time - Question 3 - Select One or More
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
Azero, when θ=0Bπr2Bω2R when θ=0Cπr2Bω2R when θ=π6Dπr2Bω4R when θ=π6
Current loop in a uniform magnetic field
View SolutionA rectangular loop of wire shown below is coplanar with a long wire carrying current I.
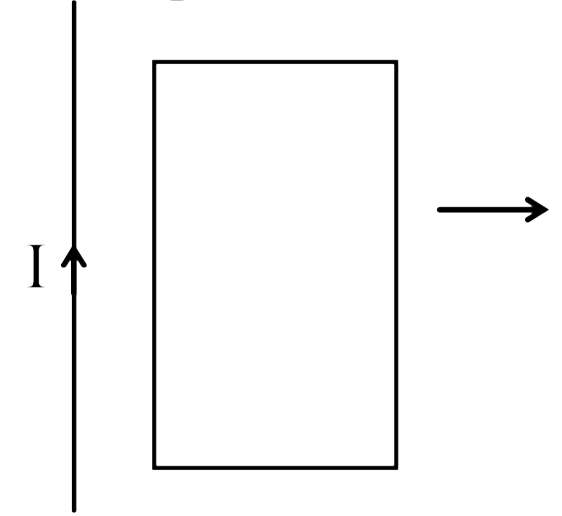The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionA triangle loop as shown in the figure is started to being pulled out at t=0 from a uniform magnetic field with a constant velocity v.Total resistance of the loop is constant and equals to R.Then the variation of power produced in the loop with time will be:
View SolutionA square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
View Solution