Show that a gun will shoot woll shoot three times as hith when elevated at an angle of 60∘ as when fired at an angle 30∘ but will have the same horizontal rande.
Let (u) be the velocity of shot fired from a gun at an angle θ with the horizontal. Then
Max. height , H=u2sin∘θ2g ,
Horizontal range, R=9u2sin2θ)g
When θ=30∘ ,
H1=u2sin230∘2g=u2sin×1/42g=u28g
R1=u2sin2×30∘g=u2sin60∘g=u2√3g2
Whem θ=60∘,
H_2 = (u^2 sin ^2 60^@)/(2 g) = (u^2 (sqrt 3//2)^2)/(2 g) = (u^2 sqrt 3)/ (g 2)<br> R_2 = (u^2 sin 2 xx 60^@_ /g =( u^2 sin 120^@_ g = (3 u^@)/( 8 2)<br>Fromabove,we⊥etˆ R_1 = R_2and<br> H_2 /H_1 = (23 u^2 //8 g)/(u^2 // 8 g/(u^1 // 8 g) = 3 or H_2 =3 H_1 (Proved).
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 5 Short answer
6 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 6 Short answer
8 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Short answer
37 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
Show that a given gun will shoot three times as high when elevated at an angle of 60∘ as when fired at angle of 30∘ but will carry the same distance on a horizontal plane.
View SolutionA gun kept on a striaght horizontal is used to hit a car, traveling along the same road away form the gun with a unfrom speed 20m/s. The car is at a distance 0f 160m from the gun, when the gun is fired at an angle of 45∘ with the horizontal Find the distance of the car from the gun when the shell hits it and the speed of projection of the shell from the gun.
View Solution
Knowledge Check
It was calculated that a shell when fired from a gun with a certain velocity and at an angle of elevation 5π/36 radius should strike a given target. In actual practice it was found that a hill just intervened in the trajectory. At what angle of elevation should the gun be fired to hit the target ?
A5π36RadB11π36RadC7π36RadD13π36RadTwo bodies are projected with the same velocity. If one is projected at an angle of 30∘ and the other at an angle of 60∘ to the horizontal, the ratio of the maximum heights reached is
A3:1B1:3C1:2D2:1A particle is projected with speed 'u' at an angle 60∘ with horizontal, then find the speed when its angle with horizontal changes to 30∘ .
Au2Bu√32Cu√3Du√3
A gun fires a shell and recoils horizontally . If the shell travels along the barrel with speed v , the ratio of speed with which the gun recoils if (i) the barrel is horizontal (ii) inclined at an angle of 30∘ with horizontal is
View SolutionA car is traveling on a straight level track with a uniform speed of 25 m/s. When the car is moving away from a gun at the same level at a distance of 1500 m the gun is fired at an angle of 45∘. Find the distance of the car (kilometers) from the gun when it is hit.
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
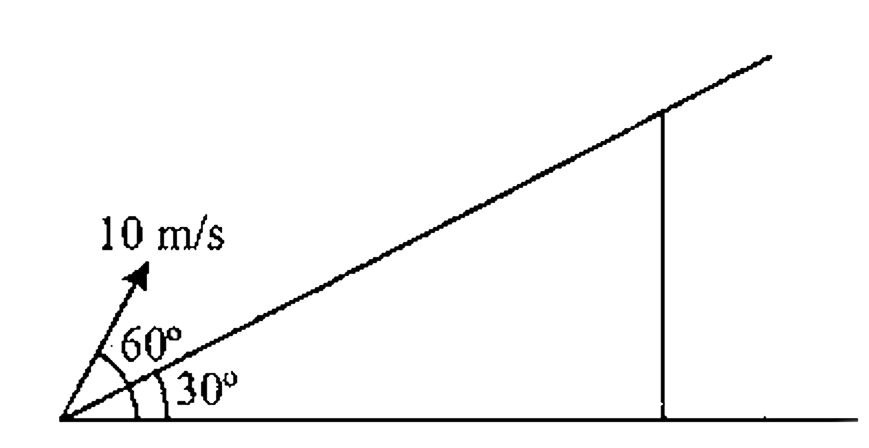
View SolutionA particle at a height h from the ground is projected with an angle 30∘ from the horizontal, it strikes the ground making angle 45∘ with horizontal. It is again projected from the same point with the same speed but with an angle of 60∘ with horizontal. Find the angle it makes with the horizontal when it strikes the ground
View SolutionTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View Solution
