Define trajectory of a projectile and hence derive equation of motion of the projectile when projected at an angle θ with horizontal direction.
Step by step video & image solution for Define trajectory of a projectile and hence derive equation of motion of the projectile when projected at an angle theta with horizontal direction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 5 Short answer6videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 6 Short answer8videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Short answer37videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is projected from the top of a tower of height h with a speed u at an angle θ above the horizontal .
T1=Time taken by the projectile to reach the height of tower again .
T2=Time taken by the projectile to move at right angle to initial direction of motion .
V1=Speed of the projectile when it moves at an angle θ/2 with the horizontal .
V2=Speed with projectile strikes the ground .
.
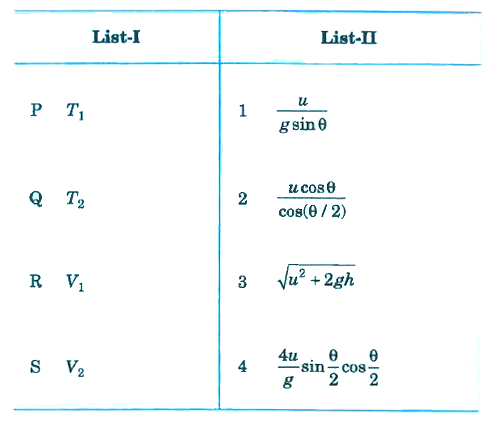APQRS4123BPQRS1234CPQRS2413DPQRS2134 - Question 2 - Select One
The question given below consist of an assertion and the reason . Use the following key to choose appropriate answer:
Assertion: Range of projectile motion is same when particle is projected at an angle θ with the horizontal or at an angle (90∘−θ) with the horizontal .
Reason : Range of projectile motion depended only on the angle of projection.AIf both assertion and reason are correct and reason is a correct explanation of the assertionBIf both assertion and reason are correct but reason is not the correct explanation of assertion .CIf assertion is correct but reason is incorrect .DIf both assertion and reason are incorrect . - Question 3 - Select One
The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
Asin1xBcos−1xCsin−1(1/x)Dcos−1(1/x)
Trajectory Of Horizontal Projectile
View SolutionFor a projectile projected at an angle _____the maximum height and horizontal range are equal.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionFind (a) time of flight , (b) Max.height (c ) Horizontal range of projectile projected with speed (v) making an angle θ with the horizontal direction from ground.
View Solution