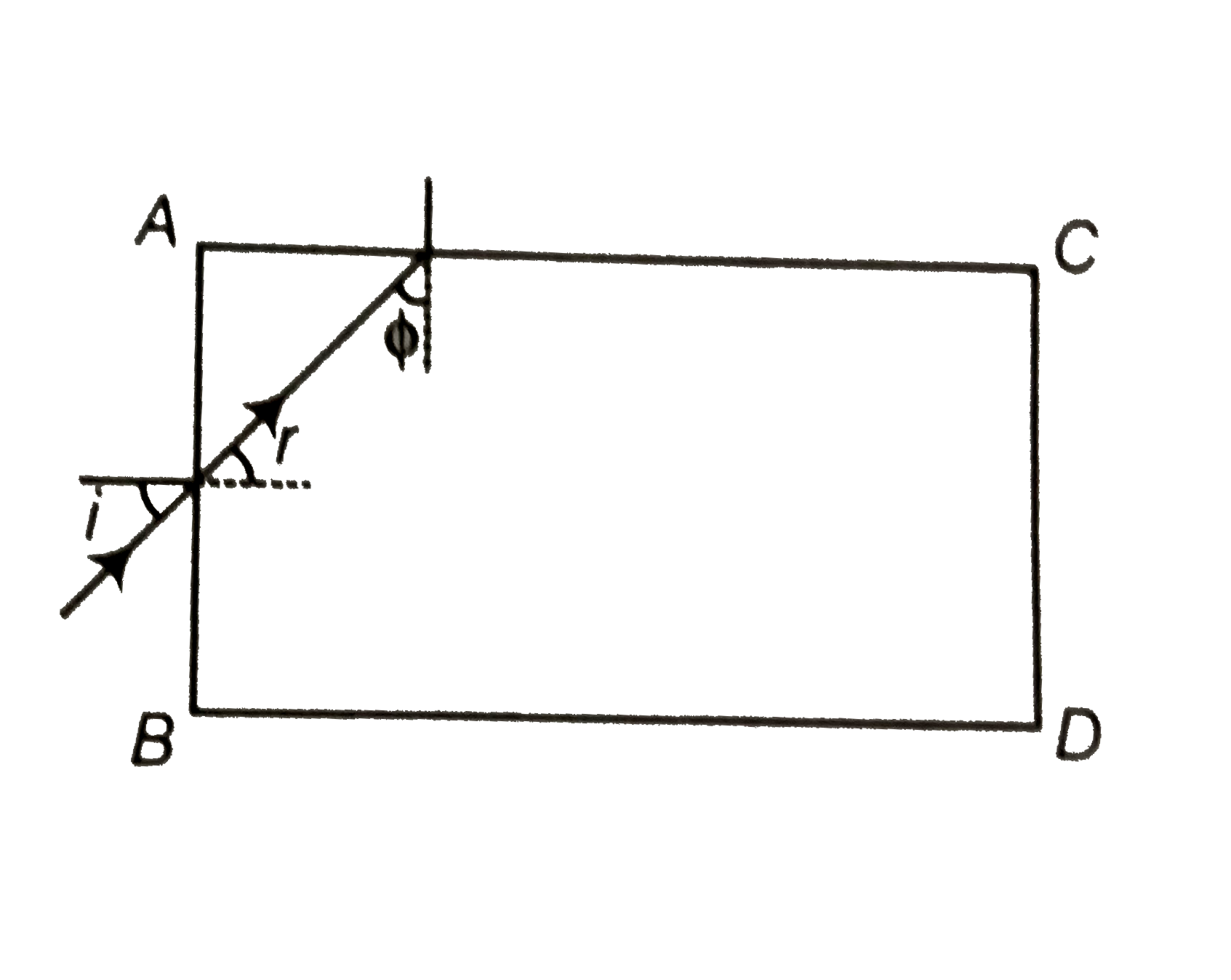
Show that for a material with refractive index μ≥√2, light incident at any angle shall be guided along a length perpendicular to the incident face.
Any ray entering at an angle I shall be guided along AC if the angle ray makes with the face AC (ϕ) is greater than the critical angle as per the principle of total internal reflection ϕ+r90∘ , therefore sinϕ=cosr
⇒ sinϕ≥1μ
⇒ cosr≥1μ
or 1−cos2r≤1−1μ2
i.e., sin2r≤1μ2
i.,e, sin2r≤1−1μ2
since, sini−μsinr
1μ2sin2i≤1−1μ2orsin2i≤μ2−1
when i=π2
Then, we have smallest angle ϕ
If that is greater than the critical angle, then all other angles of inidence shall be more than the ciritical angle
Thus 1≤μ2−1
or μ2≥2
⇒ μ≤√2
This is the required result.
Topper's Solved these Questions
- NUCLEIBook:NCERT EXEMPLARChapter:NUCLEIExercise:Nuclei
Explore 40 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITBook:NCERT EXEMPLARChapter:SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITExercise:Semiconductor Electronics: Material,Devices And Simple Circuit
Explore 26 Videos
Similar Questions
Monochromatic light falls at an angle of incidence i on a slab of a transparent material (refractive index μ). If reflected and refracted rays are mutually perpendicular, find the relation between μ and i.
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?

View Solution
Knowledge Check
Unpolarised light is incident from air on a plane surface of a meterial of refractive index 'μ'. At a particular angle of incidence 'I', it is found that the reflected and refracted rays are perpendicular to each other.
Which of the following options is correct for this situation?Ai=sin−1(1μ)BReflected light is polarised with its electric vector perpendicular to the plane of incidenceCReflected light is polarised with its electric vector parallel to the plane incidenceDi=tan−1(1μ)A ray of light falls on a transparent glass slab of refractive index √2. If the reflected and refracted rays are mutually perpendicular, then the angle of incidence is
Atan−1(√32)Bsin−1(√23)Ctan−1(√2)Dsin−1(√3)Unpolarised light is incident from air on a plane surface of a meterial of refractive index 'μ'. At a particular angle of incidence 'I', it is found that the reflected and refracted rays are perpendicular to each other.
Which of the following options is correct for this situation?A(a) i=tan−1(1μ)B(b) Refracted light is polarized with its electric vector parallel to the plane of incidenceC(c) i=sin−1(1μ)D(d) Refracted light is polarized with its electric vector perpendicular to the plane of incidence
Unpolarised light is incident on a plane surface heaving refractive index √3. The angle of incidence at which reflected and refracted rays would become perpendicular to each other is
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View SolutionA ray of light passes from vacuum into a medium of refractive index n . If the angle of incidence is twice the angle of refraction , then the relation between the angle of incidence and the refractive index is
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
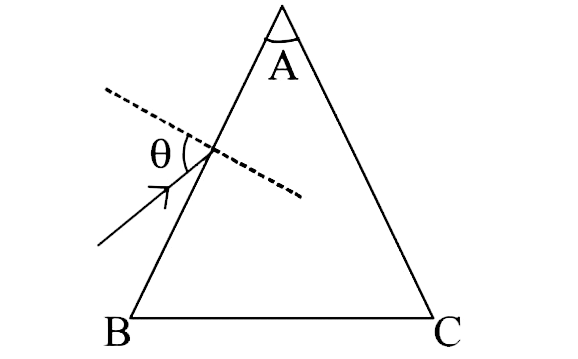
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
View Solution