Show that if a rod held at angle θ to the horizontal and released, its lower end will not slip if the friction coefficient between rod and ground is greater than 3sinθcosθ1+3sin2θ

Point A is momentarily at rest.
α=mg(l)2cosθml23=32gcosθl
∴aC=l2α=34gcosθ
Now μN=max
or μN=maCsinθ
or μN=34mgsinθcosθ ..(i)
further mg−N=may
or N=mg−maC.cosθ
or N=mg−34mgcos2θ .(ii)
dividing eq. (i) by eqs. (ii), we get
μ=34sinθcosθ1−34cos2θ=3sinθcosθ4−3cos2θ
=3sinθcosθ1+3sin2θ
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
A sphere can roll without slipping on a surface inclined at an angle θ if the fiiction coefficient is more than (2/7)g sin θ Suppose the friction coefficient is (l/7)g sin θ If a sphere is released from rest on this incline then which ofthe following are possible situations:
AIt will stay at restBItwill make pure translational motionCIt will translate and rotate about the centreDThe angular momentum of the spheres about its centre will remain constant
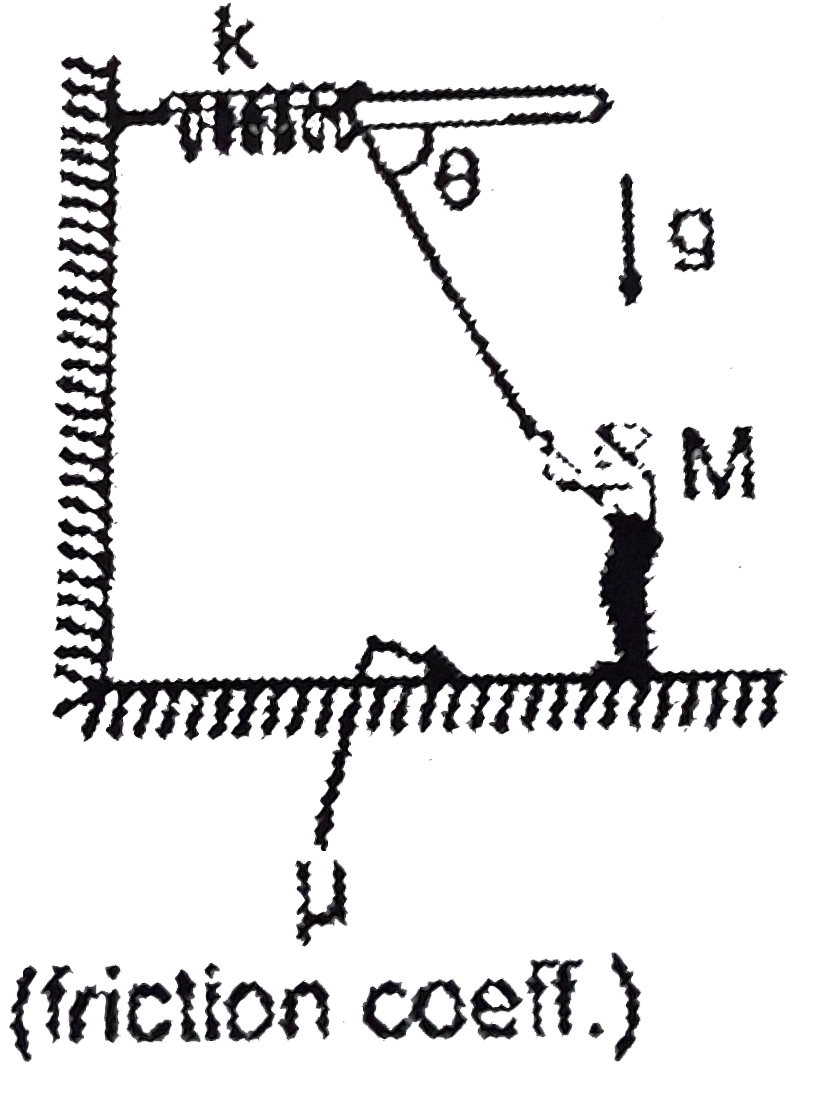
A man with mass M has its string'.attached to one end. of a spring which can move without friction along a horizontal, overhead fixed rod. The other end of the spring is fixed to a, wall. The spring constant is k. The string is massless and inextensible and it maintains a constant angle θ with the, overhead rod, even when the man moves. There is friction, iwith coefficient μ between the man and the ground. What is, the maximum distance (in m ) that the man moving slowly can stretch the spring beyond its natural length?
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionProve sin3θ+cos3θsinθ+cosθ=1−sinθcosθ
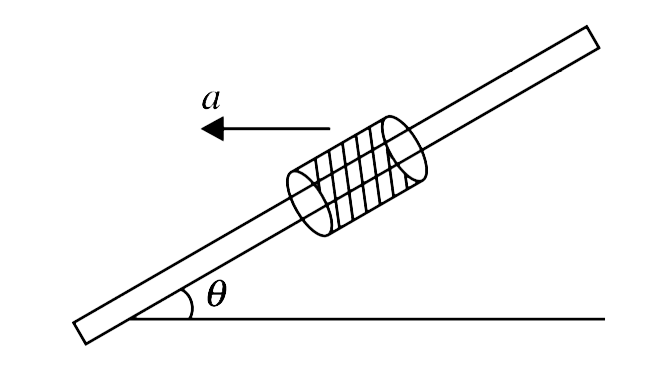
View SolutionA rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
View Solution
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is
View Solution

