
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
The correct Answer is:a=g4√3
Topper's Solved these Questions
Similar Questions
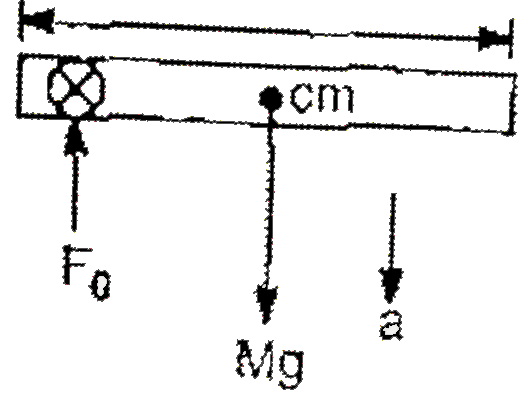
A uniform slender rod of length L and mass M is pivoted at one end. It is held horizontal and releasaed. Assume the pivot is frictionless. Find .
(a) the angular acceleration of the rod immediately after it is released, and
(b) the force F0 exerted on the rod by the pivot immediately after release.
View SolutionA ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View Solution
Knowledge Check
A ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−
 AF3B2F3CF4DZero
AF3B2F3CF4DZeroA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZeroA particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m and radius 'r' . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after
 Ag4rBg6rCg8rDg2r
Ag4rBg6rCg8rDg2r
A ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

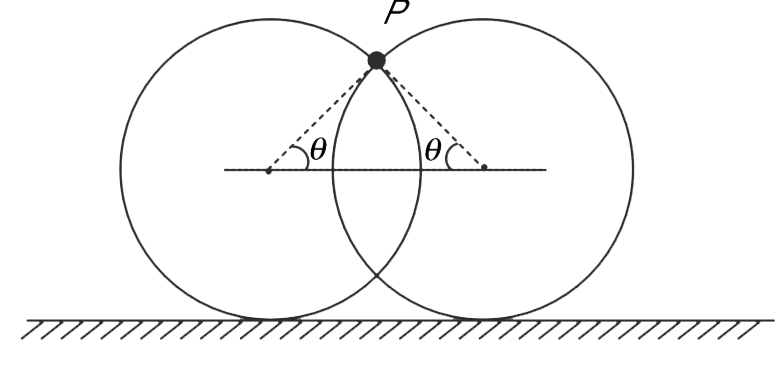
View SolutionTwo identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionA ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
View Solution
