Show that if the room temperature changes by a small amount from T→T+△T, the fundamental frequency of an organ pipe changes from v→v+△v,where<br>(/_\v)/v=1/2(/_\T)/T.
The correct Answer is:A
We know that f∝√T
According to the questioin
f+△f∝√△T+T
→f+△ff=√△T+TT)
→1+△ff=(1+△TT)12
=1+12△TT
…….(¬≤ct∈gotherterms)
→△ff=(12)△TT
Topper's Solved these Questions
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Objective -2
5 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises
35 Videos
Similar Questions
The room temperature charges by a small amount from T to T+ΔT (on Kelvin scale). The fundamental frequency of organ pipe changes from f to f+Δf, then
View SolutionFor a sample of n mole of a perfect gas at constant temperature T (K) when its volume is changed from V1 to V2 the entropy change is given by
View Solution
Knowledge Check
A gas at initial temperature T undergoes sudden expansion from volume V to 2V. Then -
AThe process is adiabaticBThe process is isothermalCThe work done in this process is nRT lne(2) where n is the number of moles of the gas.DThe entropy in the process does not changeTwo open organs pipes of fundamental frequencies v1 and v2 are joined in series. The fundamental frequency of the new pipe so obtained will be
Aυ1+υ2Bυ1υ2(υ1+υ2)Cυ1υ2υ1+υ2D√(υ21+υ22)Pressure P, volume V and temperature T for a certain gas are related by P=AT−BT2V, where A and B are constants .The work done by the gas as its temperature change from T1 to T2 while pressure remaining constant is
AA−B2(R2−T1)BA(T2−T1)−B(T22−T21)CA2(T22−T21)−B3(T32−T31)DA(T2−T1)−B3(T2−T1)3
The voltage time (V-t) graph for triangular wave having peak value V0 is as shown in figure.The rms value of V in time interval from t=0 to T/4 is
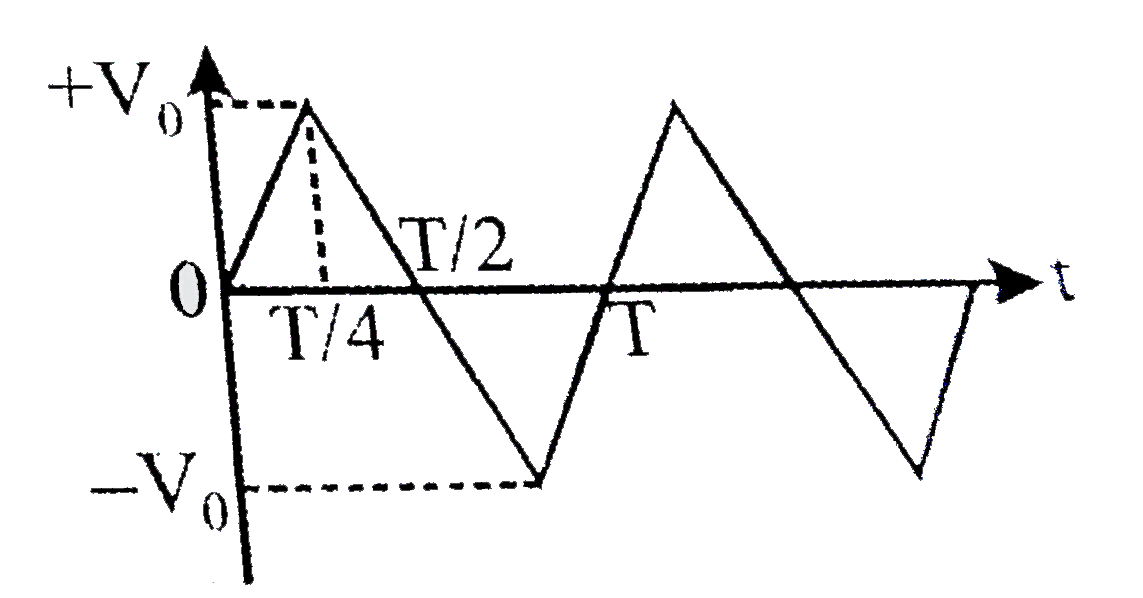
View SolutionOne mole of an ideal monoatomic gas undergoes the process T=T0+4V, where T0 is initial temperature. Find
(i) Heat capacity of gas as function of its volume.
(ii) The amount of heat transferred to gas if its volume increases from V0 to 4V0.
View SolutionThe velocity of a particle at an instant "t" is v=u+at ,where u is initial velocity and a is constant acceleration.The v -t graph are
View SolutionPressure P, voluume V and temperature T for a certain gas are related by P=AT−BT2V where A and B are constant. The work done by the gas as its temperature change from T1 to T2 with pressure remaining constant is
View SolutionA generator produces a voltage that is given by V=240 sin 120t, where t is in seconds. The frequency and rms voltage are (1)
View Solution
