Show that the angle made by the string with the vertical in a conical pendulum is given by cosθ=gLω2 , where L is the string and ω is the angular speed.
The correct Answer is:A
To show that the angle made by the string with the vertical in a conical pendulum is given by the equation:
cosθ=gLω2
where L is the length of the string and ω is the angular speed, we can follow these steps:
Step 1: Understanding the Setup
Consider a conical pendulum where a mass m is attached to a string of length L. The mass moves in a horizontal circle while the string makes an angle θ with the vertical.
Step 2: Forces Acting on the Mass
The forces acting on the mass are:
1. The gravitational force →Fg=mg acting downwards.
2. The tension →T in the string acting along the string at an angle θ to the vertical.
Step 3: Resolving Forces
We can resolve the tension T into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
Step 4: Applying Newton's Second Law
In the vertical direction, the forces must balance since there is no vertical acceleration:
Tcosθ=mg(1)
In the horizontal direction, the mass is undergoing circular motion, so we apply the centripetal force equation:
Tsinθ=mv2r(2)
where r is the radius of the circular path.
Step 5: Relating Radius to Angle
The radius r can be expressed in terms of the length of the string and the angle θ:
r=Lsinθ
Step 6: Substituting for r
Substituting r into equation (2):
Tsinθ=mv2Lsinθ
Step 7: Expressing Velocity in Terms of Angular Speed
The linear velocity v can be related to the angular speed ω:
v=rω=Lsinθ⋅ω
Substituting this into the equation gives:
Tsinθ=m(Lsinθ⋅ω)2Lsinθ
This simplifies to:
Tsinθ=mLsinθ⋅ω2
Step 8: Cancelling sinθ
Assuming sinθ≠0, we can cancel sinθ from both sides:
T=mLω2(3)
Step 9: Substituting T in Equation (1)
Now substitute equation (3) into equation (1):
mLω2cosθ=mg
Step 10: Simplifying the Equation
Dividing both sides by m:
Lω2cosθ=g
Step 11: Final Rearrangement
Rearranging gives:
cosθ=gLω2
This is the required proof.
Consider a conical pendulum where a mass m is attached to a string of length L. The mass moves in a horizontal circle while the string makes an angle θ with the vertical.
The forces acting on the mass are:
1. The gravitational force →Fg=mg acting downwards.
2. The tension →T in the string acting along the string at an angle θ to the vertical.
We can resolve the tension T into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
In the vertical direction, the forces must balance since there is no vertical acceleration:
Tcosθ=mg(1)
Tsinθ=mv2r(2)
where r is the radius of the circular path.
The radius r can be expressed in terms of the length of the string and the angle θ:
r=Lsinθ
Substituting r into equation (2):
Tsinθ=mv2Lsinθ
The linear velocity v can be related to the angular speed ω:
v=rω=Lsinθ⋅ω
Substituting this into the equation gives:
Tsinθ=m(Lsinθ⋅ω)2Lsinθ
This simplifies to:
Tsinθ=mLsinθ⋅ω2
Assuming sinθ≠0, we can cancel sinθ from both sides:
T=mLω2(3)
Now substitute equation (3) into equation (1):
mLω2cosθ=mg
Dividing both sides by m:
Lω2cosθ=g
Rearranging gives:
cosθ=gLω2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective
14 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Fig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
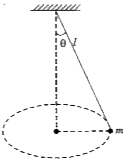
View SolutionThe angle made by the string of a simple pendulum with the vertical depends on time as θ=π90sin[(πs−1)t]. Find the length of the pendulum if g=π2ms−2
View Solution
Knowledge Check
A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
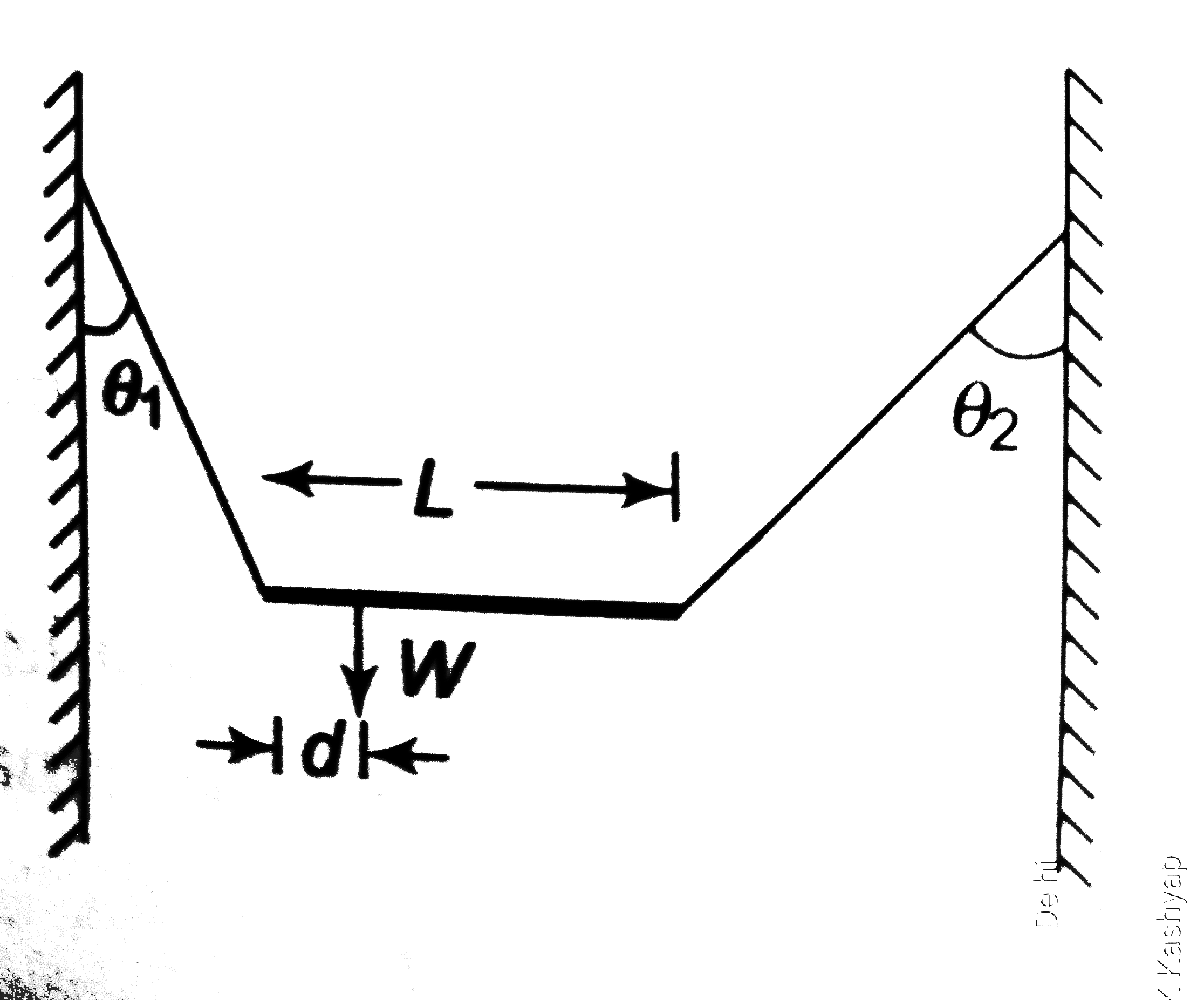 .AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
.AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)A simple pendulaum consists of a small mass suspended from a string that is fixed at its upper end and has negligible mass. The length of time, t second, for complete swing of a simple pendulum can be modeled by the equation t=2π√L32, where L is the length, in feet, of the string. If the time required for a complete swing of Pendulum 1 is triple the time required for a complete swing of Pendulum 2, the length of Pendulum 1's string is how many times the length of Pendulum 2's string?
A13B3C6D9
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA non-uniform bar weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from its left end is
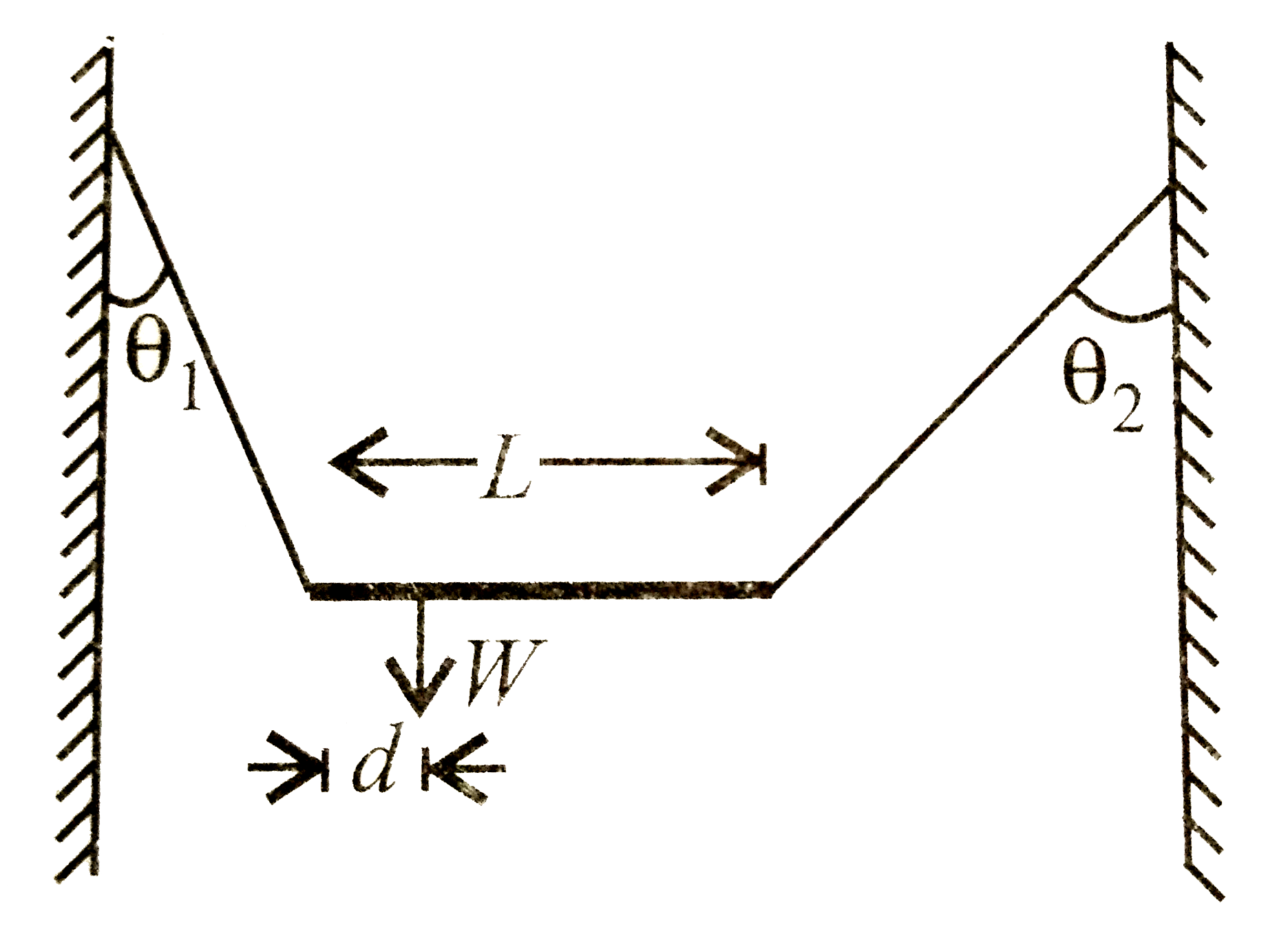
View SolutionIf the string of a conical pendulum makes an angle θ with horizontal, then square of its time period is proportional to
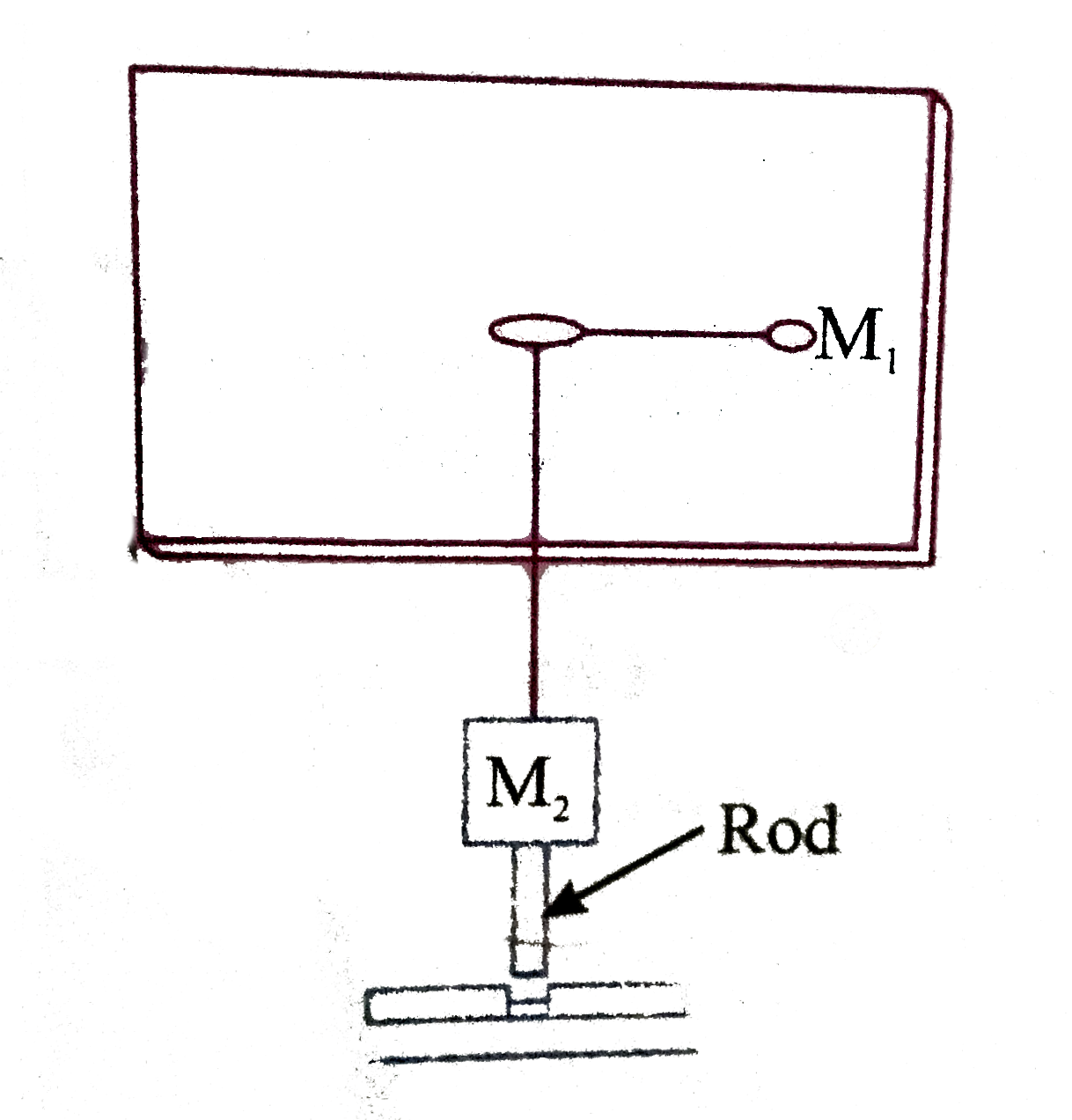
View SolutionFor the arrangement in the Figure, the particle M1 attached to one end of string which moves on a horizantal table in a circle of radius l2 (where l is the length of the string) with constant angular speed ω. The other end of the string attached to to mass M2 which rest on a vertical rod. When the rod collapse, the acceleration of mass M2 at that instant
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View Solution
