A non-uniform bar weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from its left end is
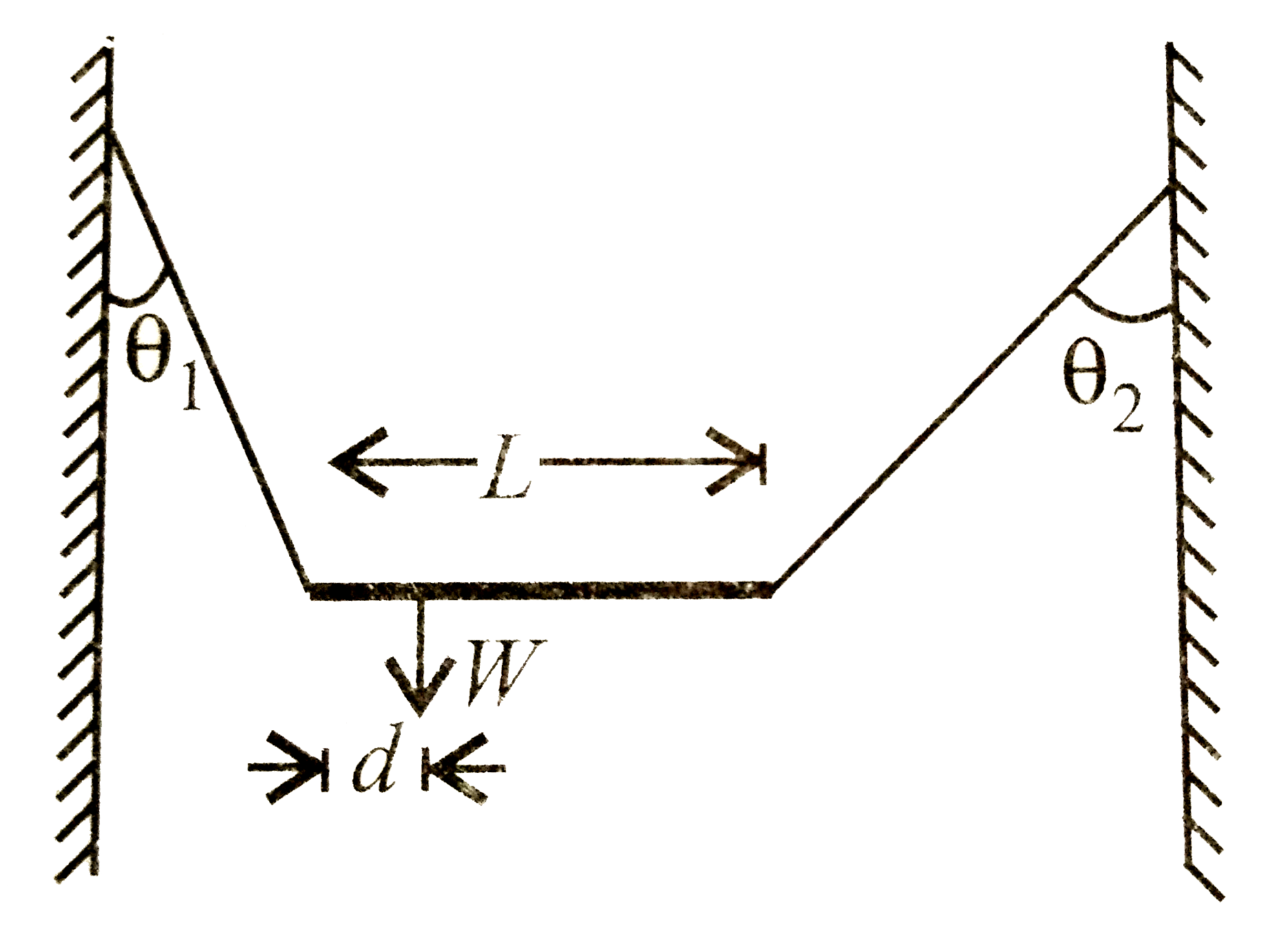
As it is clear from Fig., θ1=36.9∘,θ2=53.1∘.
It T1,T2 are the tensions in the two strings, then for equilibrium along the horizontal,
T1sinθ1=T2sinθ2
or T1T2=sinθ2sinθ1=sin53.1∘sin36.9∘
=0.74040.5477=1.3523
Let d be the distance of centre of gravity C of the bar from the left end.
For rotaional equilibrium about C,
T1cosθ1×d=T2cosθ2(2−d)
T1cos36.9∘×d=T2cos53.1∘(2−d)
T1×0.8366d=T2×0.6718(2−d)
Put T1=13523T2 and solve to get
d=0.745 m
τ=I1α1=I2α2
or α1α2=I2I1=(2/5)MR2MR2=25
or α2=52α1.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
A non-uniform bar weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from its left end is

View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View Solution
Knowledge Check
A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
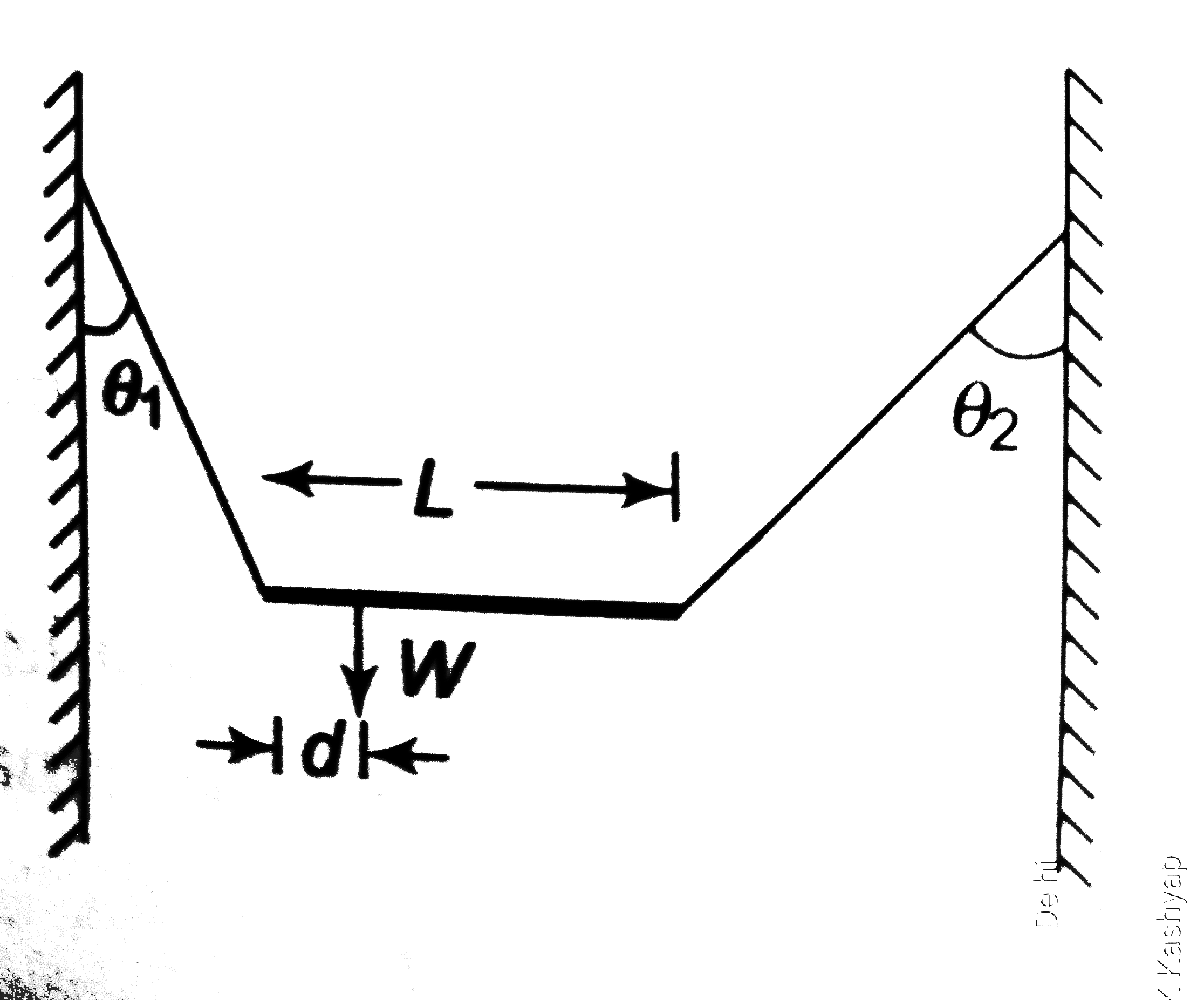 .AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
.AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
A uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
View SolutionA uniform sphere of weight W and radius 3 m is being held by a frictionless wall as shown in the figure. The tension in the string will be (length of the string is 2m):
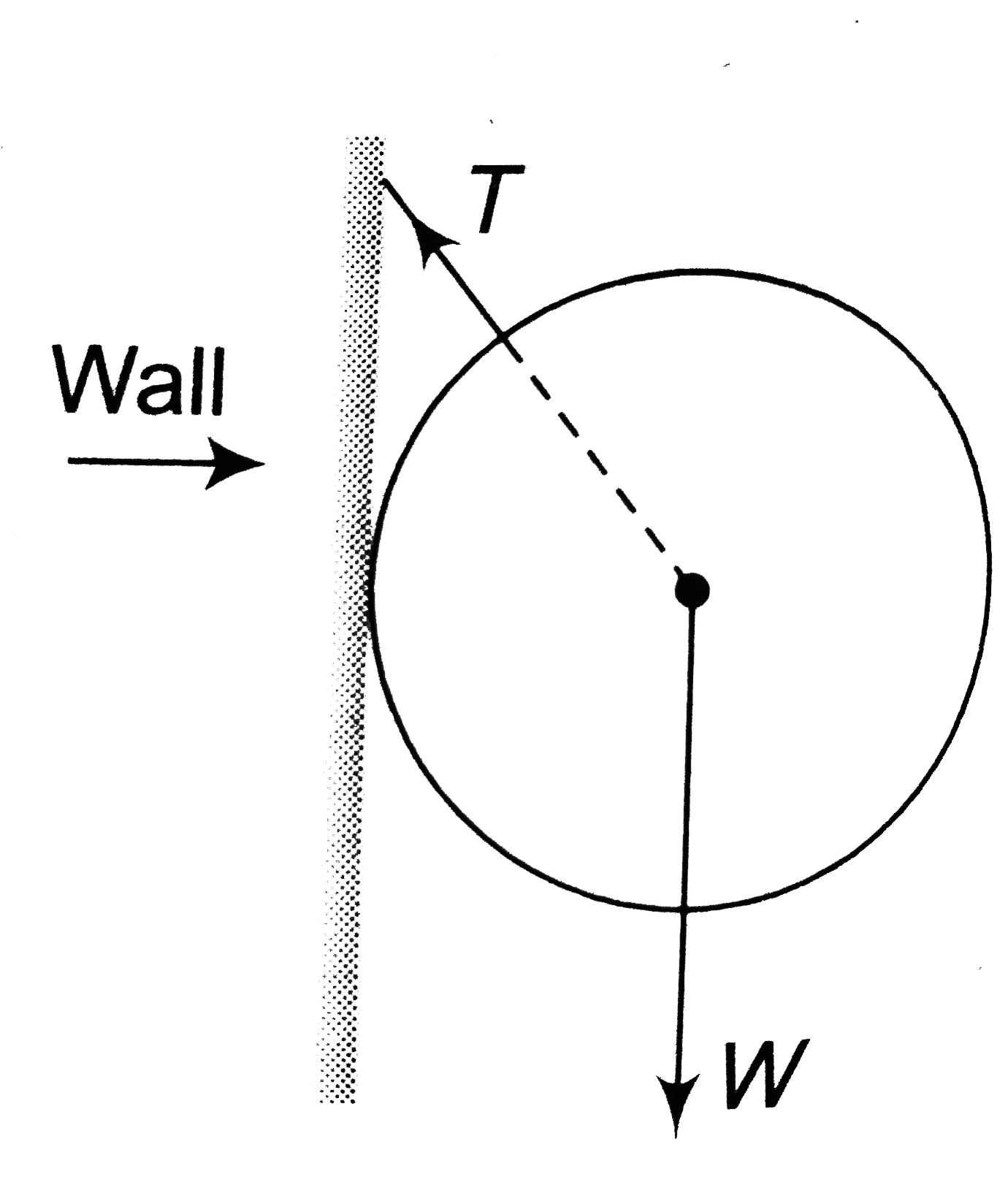
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View Solution
A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View SolutionA uniform rod of length l and mass m is suspended from one end by inextensible string and other end less lies on smooth ground. The angle made by the rod with vertical is θ=sin−1(1/√3). If N1 and N2 represent the contact force from ground on rod just before and just after cutting the string then the ratio of N1/N2 is 0.25 x. Find the value of x.

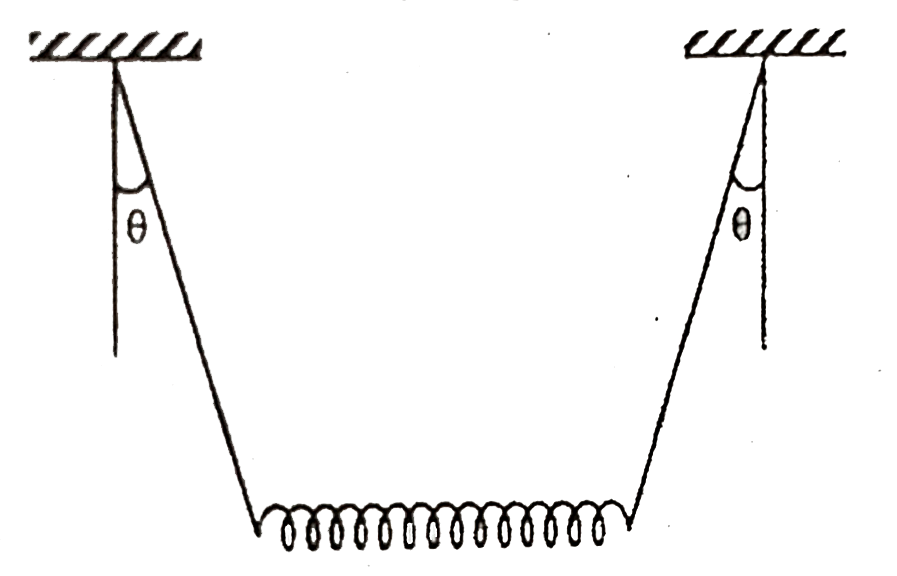
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
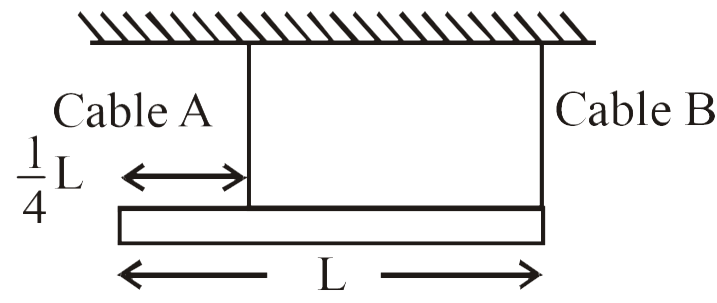
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
View Solution
