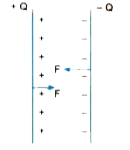
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to $\frac{1}{2} Q E$ , where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor $\frac{1}{2}$ .

Text Solution

Verified by Experts

Consider a parallel plate capacitor with one plate having + Q charge and the other having - Q charge. Let F be the force between them. If the plates be displaced by a small distance dl, the work done dW = Fdl. This work results in the change in electrostatic potential energy of the capacitor.
$∴$ Energy density of capacitor $u = \frac{1}{2} ε_{0} E^{2}$
and charge in volume = A.dl
$∴$ Change in potential energy $d u = \frac{1}{2} ε_{0} E^{2} . A d l$
Thus, we have $F d l = \frac{1}{2} ε_{0} E^{2} A d l$
$\Rightarrow F = \frac{1}{2} ε_{0} E^{2} A = \frac{1}{2} ε_{0} E . A . E = \frac{1}{2} (ε_{0} \frac{σ}{ε_{0}} A) E = \frac{1}{2} (σ A) E = \frac{1}{2} Q E$
The physical origin of the factor $\frac{1}{2}$ in the above formula for force lies in the fact that just between the plates of capacitor electric field is E but just outside E = 0. Hence, average value $\frac{E}{2}$ contributes to the force.

Updated on:21/07/2023

Force of attraction between the plates of a parallel plate capacitor is
A $\frac{q^{2}}{2 ε_{0} A K}$
B $\frac{q^{2}}{ε_{0} A K}$
C $\frac{q}{2 ε_{0} A}$
D $\frac{q^{2}}{2 ε_{0} A^{2} K}$
The surface charge densities on two square plates of a parallel plate capacitor are to $+ σ and - σ$ respectively. What is the magnitude of the electric field in the region between the plates?
A $\frac{σ}{2 ε_{0}}$
B $\frac{σ}{ε_{0}}$
C0
DNone of these
A parallel plate capacitor has an electric field of $10^{5} V / m$ between the plates. If the charge on the capacitor plate is $1 μ C$ , the force on each capacitor plate is
A0.5 N
B0.05 N
C0.005 N
D5 N