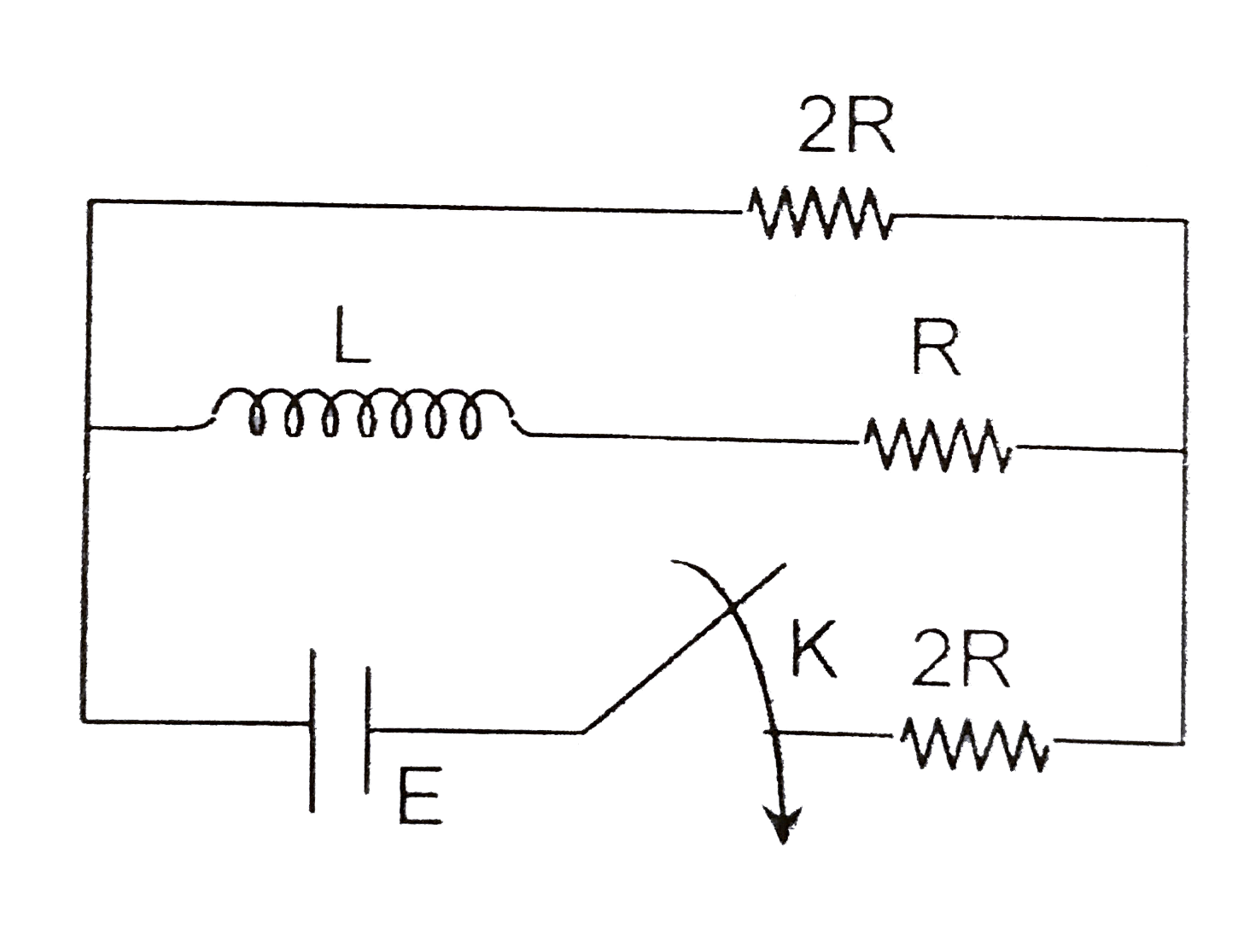
Show that the sum of instantaneous currents during growth and decay of current in LR circuit is independent of time.
Video Solution
Text Solution
During growth of current in LR circuit,
Ig=I0(1−e−Rt/L) and
during decay of current in LR circuit,
Id=I0e−Rt/L
Sum of the currents at any instant t,
Ig+Id=I0(1−e−Rt/L+e−Rt/L)=I0
which is constant, and is independent to time.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The dimensionsof "time constant" LR during growth and decay of current in all inductive circuit is same as that of
AConstantBResistanceCCurrentDTime - Question 2 - Select One
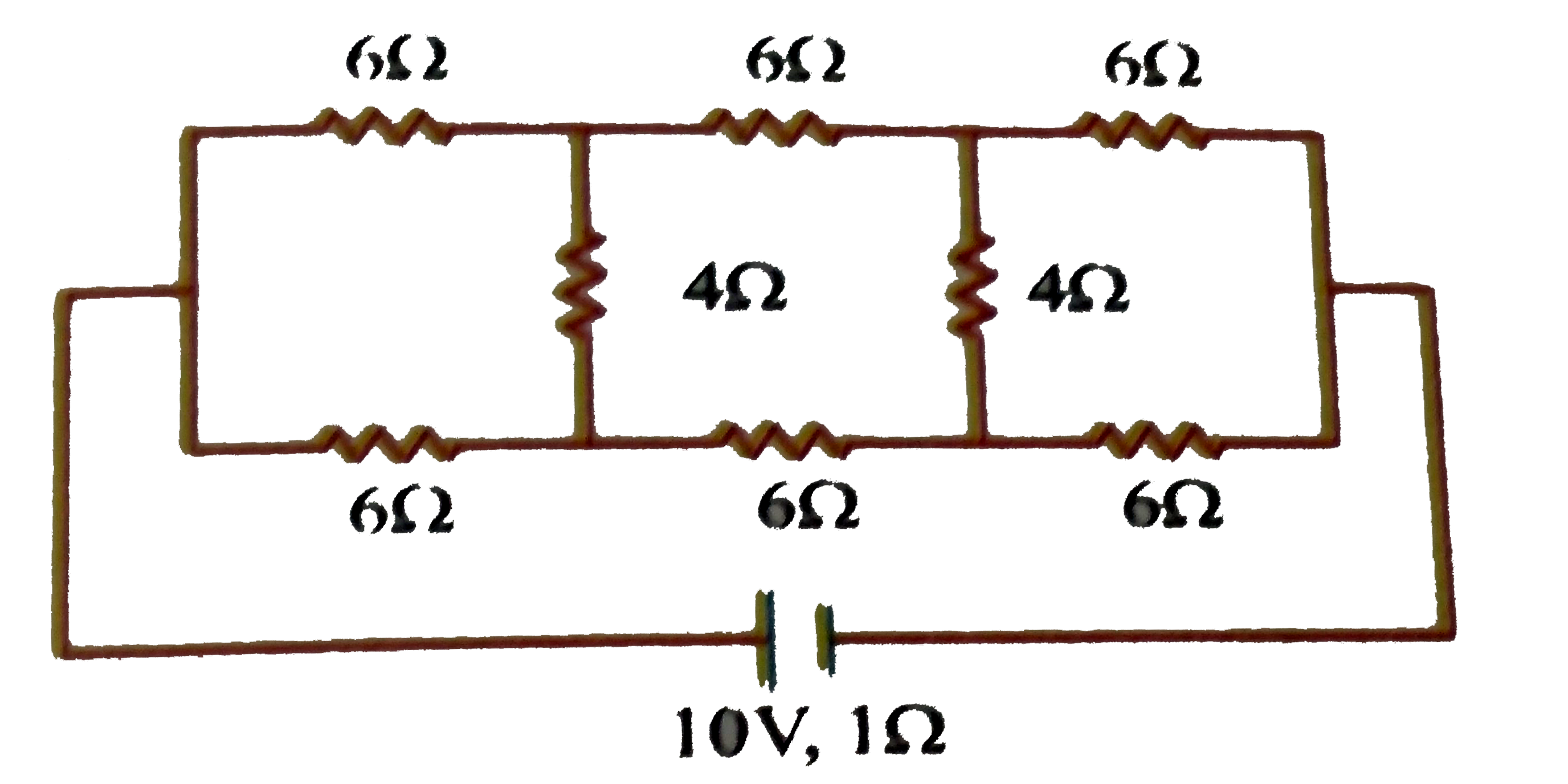
Current in the ain circuit shows isA1.5 AB0.083333333333333C0.6 AD1A - Question 3 - Select One
The ratio of time constant during current growth and current decay of the circuit shown in Figure is
 A1:1B3:2C2:3D1:3
A1:1B3:2C2:3D1:3