Show that when a string fixed at its two ends vibrates in 1 loops, 2 loops , 3 loops and 4 loops , the frequencies are in the ratio 1:2:3:4.
To show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops, and 4 loops, the frequencies are in the ratio 1:2:3:4, we can follow these steps:
Step 1: Understand the formula for frequency
The frequency of a vibrating string fixed at both ends is given by the formula:
fn=n2L√Tm
where:
- fn is the frequency of the nth harmonic,
- n is the number of loops (or harmonics),
- L is the length of the string,
- T is the tension in the string,
- m is the linear mass density of the string.
Step 2: Identify the values of n for each case
For the first four harmonics:
- For 1 loop (fundamental frequency), n=1
- For 2 loops (first overtone), n=2
- For 3 loops (second overtone), n=3
- For 4 loops (third overtone), n=4
Step 3: Write the frequencies for each case
Using the formula, we can express the frequencies for each case:
- f1=12L√Tm
- f2=22L√Tm=22L√Tm
- f3=32L√Tm
- f4=42L√Tm
Step 4: Find the ratio of frequencies
Now, we can find the ratio of these frequencies:
- The ratio f1:f2:f3:f4 can be expressed as:
f1:f2:f3:f4=12L√Tm:22L√Tm:32L√Tm:42L√Tm
Step 5: Simplify the ratio
Since 12L√Tm is common in all terms, we can cancel it out:
f1:f2:f3:f4=1:2:3:4
Conclusion
Thus, we have shown that the frequencies of the vibrating string when it vibrates in 1 loop, 2 loops, 3 loops, and 4 loops are in the ratio of 1:2:3:4.
---
The frequency of a vibrating string fixed at both ends is given by the formula:
fn=n2L√Tm
where:
- fn is the frequency of the nth harmonic,
- n is the number of loops (or harmonics),
- L is the length of the string,
- T is the tension in the string,
- m is the linear mass density of the string.
For the first four harmonics:
- For 1 loop (fundamental frequency), n=1
- For 2 loops (first overtone), n=2
- For 3 loops (second overtone), n=3
- For 4 loops (third overtone), n=4
Using the formula, we can express the frequencies for each case:
- f1=12L√Tm
- f2=22L√Tm=22L√Tm
- f3=32L√Tm
- f4=42L√Tm
Now, we can find the ratio of these frequencies:
- The ratio f1:f2:f3:f4 can be expressed as:
f1:f2:f3:f4=12L√Tm:22L√Tm:32L√Tm:42L√Tm
Since 12L√Tm is common in all terms, we can cancel it out:
f1:f2:f3:f4=1:2:3:4
Thus, we have shown that the frequencies of the vibrating string when it vibrates in 1 loop, 2 loops, 3 loops, and 4 loops are in the ratio of 1:2:3:4.
Topper's Solved these Questions
- WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WAVESEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WAVESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
7 Videos
- UNITS AND MEASUREMENTS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions
9 Videos
- WORK, ENERGY AND POWERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Long answer
1 Videos
Similar Questions
In Melde's experiment , when a string is stretched by a piece of glass it vibrates with 7l∞ps . When the glass piece is completely immersed in water the string vibrates in 9l∞ps. What is the specific gravity of glass ?
View Solutionin an experiment it was found that string vibrates in n loops when a mass M is placed on the pan. What mass should be placed on the pan to make it vibrate in 2n loops with same frequency ? ( neglect the mass of pan )
View Solution
Knowledge Check
When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
A1 : 1 : 1 : 1B1 : 2 : 3 : 4C4 : 3 : 2 : 1D1 : 4 : 9 : 16A string fixed at its both ends vibrates in 5 loops as shown in the figure. The total number of nodes and antinodes are respectively
 A5,6B6,5C7,4D4,7
A5,6B6,5C7,4D4,7
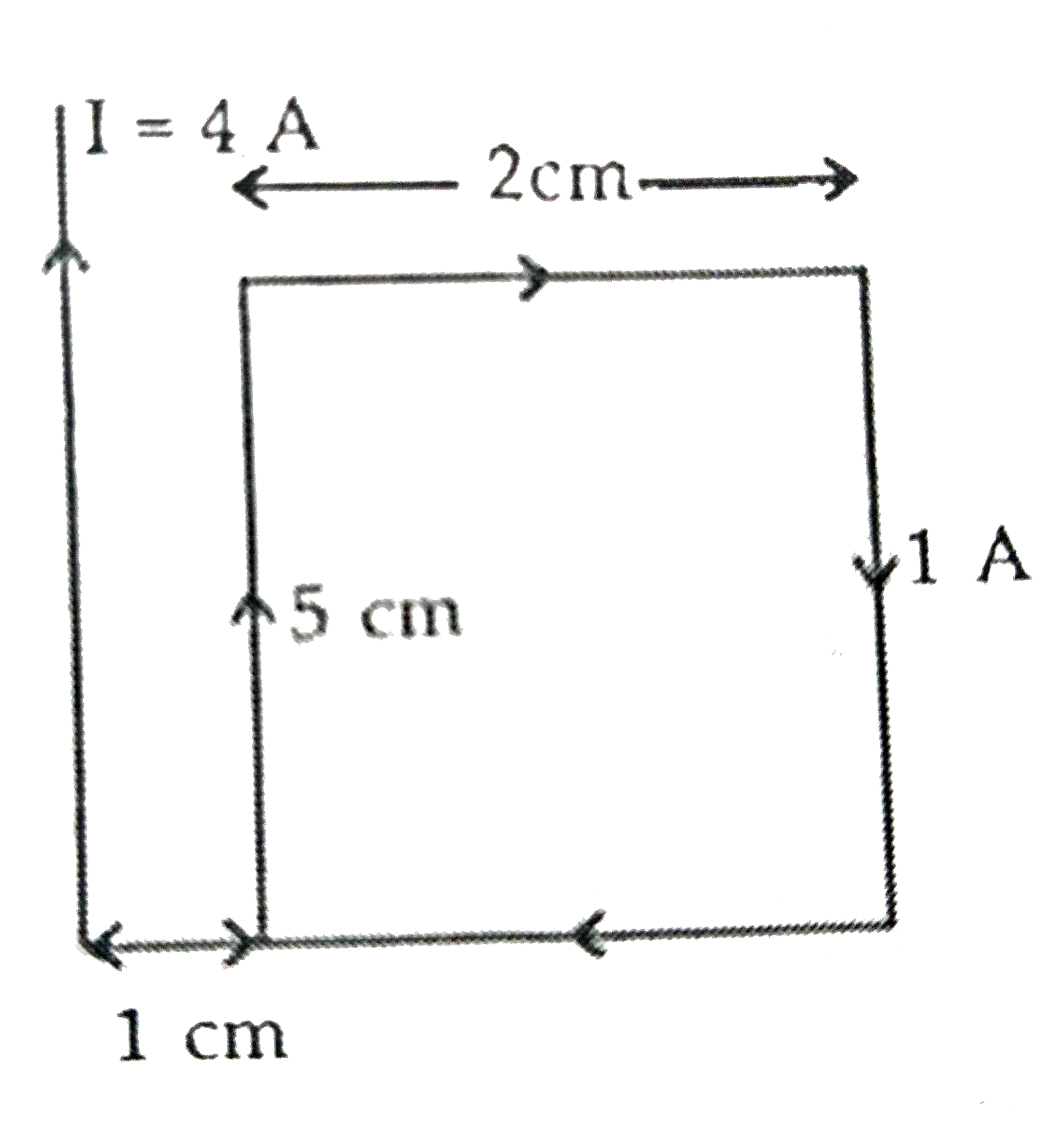
A rectangular loop of wire of size 2cm×5cm carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the end
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View Solution(A): When a stretched string vibrates in two segments, then all the vibrating particles in first half of the string are in out of phase to that of in the remaining of the string
(R): In a stationary wave the phase difference between the vibrating particles in two consecutive loops is trad.
View SolutionA rectangular loop of wire of size 4cm×10cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.

View SolutionWhen a mature mRNA was hybridized to its gene, certain loops were observed. These loops represent
View SolutionA loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

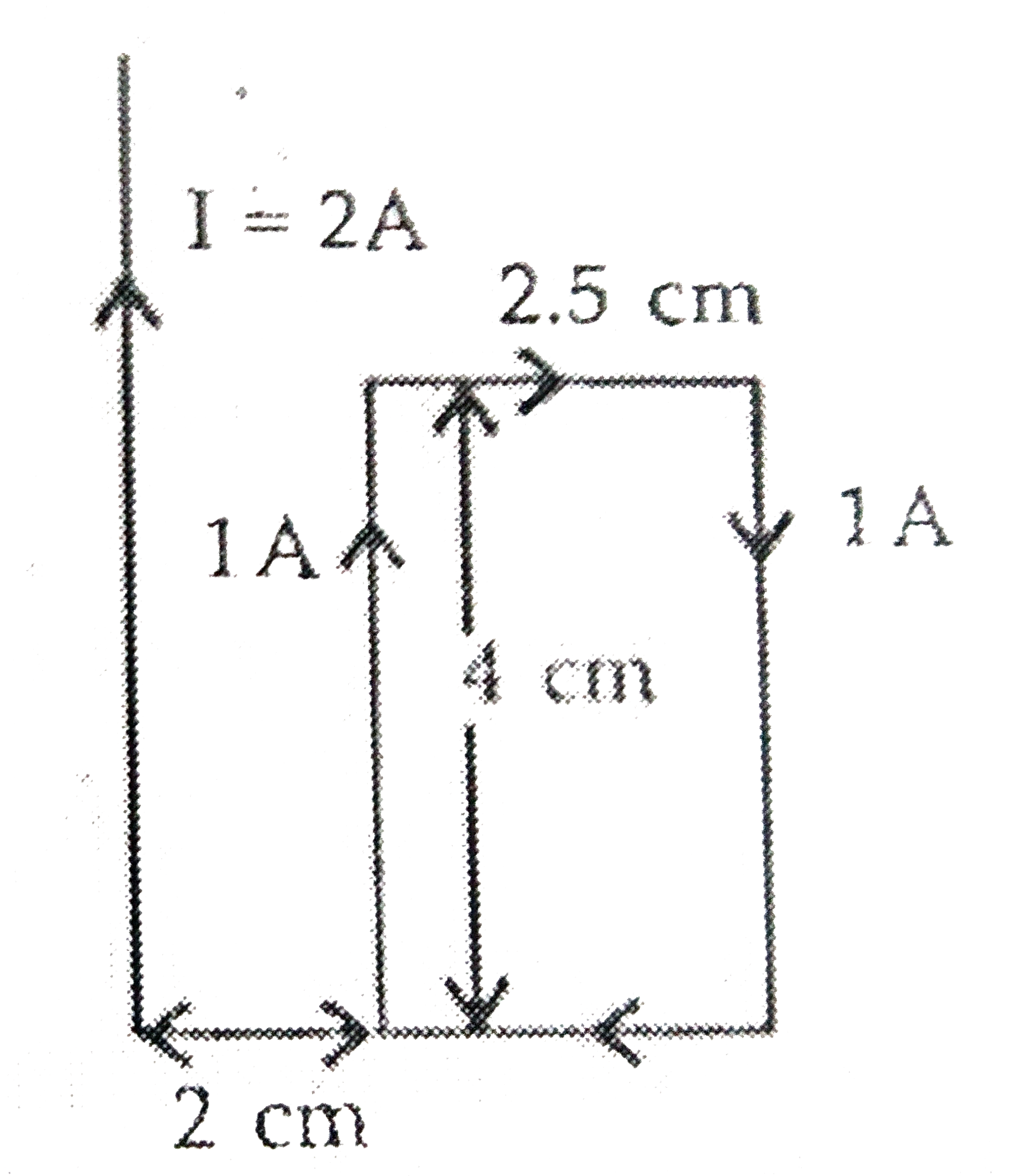
View SolutionA rectangular loop of wire of size 2.5cm×4cm carries a steady current of 1A. A straight long wire carrying 2 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View Solution
