in an experiment it was found that string vibrates in n loops when a mass M is placed on the pan. What mass should be placed on the pan to make it vibrate in 2n loops with same frequency ? ( neglect the mass of pan )
2m
m4
4M
M2
The correct Answer is:B
To solve the problem, we need to determine the mass that should be placed on the pan to make the string vibrate in 2n loops while maintaining the same frequency. Let's break down the solution step by step:
1. Understanding the relationship between loops and wavelength:
- The length of the string (L) is related to the number of loops (n) and the wavelength (λ) by the formula:
L=n⋅λ2
- This means that for n loops, the wavelength is:
λ=2Ln
2. Determining the new wavelength for 2n loops:
- When the string vibrates in 2n loops, the new wavelength (λ') becomes:
λ′=2L2n=Ln
3. Using the frequency formula:
- The frequency (f) of the wave is given by:
f=Vλ
- Since the frequency must remain constant, we have:
f=Vλ=V′λ′
- This implies:
V=f⋅λandV′=f⋅λ′
4. Relating the velocities:
- Since λ' is half of λ (λ' = λ/2), we can express the velocities as:
V′=f⋅Ln
- Thus, if λ is halved, the new velocity (V') must also change.
5. Understanding the relationship between velocity and tension:
- The velocity of a wave on a string is related to the tension (T) and the mass per unit length (μ) of the string:
V=√Tμ
- If the velocity is halved (V' = V/2), then:
V′=√T′μ
- This means:
(V2)2=T′μ
- Therefore, if V is halved, the new tension (T') becomes:
T′=T4
6. Relating tension to mass:
- The tension in the string is directly proportional to the mass (M) placed on the pan:
T∝M
- Therefore, if the new tension is T' = T/4, then the new mass (M') that should be placed on the pan is:
M′=M4
Final Answer:
To make the string vibrate in 2n loops with the same frequency, the mass that should be placed on the pan is:
M4
- The length of the string (L) is related to the number of loops (n) and the wavelength (λ) by the formula:
L=n⋅λ2
- This means that for n loops, the wavelength is:
λ=2Ln
- When the string vibrates in 2n loops, the new wavelength (λ') becomes:
λ′=2L2n=Ln
- The frequency (f) of the wave is given by:
f=Vλ
- Since the frequency must remain constant, we have:
f=Vλ=V′λ′
- This implies:
V=f⋅λandV′=f⋅λ′
- Since λ' is half of λ (λ' = λ/2), we can express the velocities as:
V′=f⋅Ln
- Thus, if λ is halved, the new velocity (V') must also change.
- The velocity of a wave on a string is related to the tension (T) and the mass per unit length (μ) of the string:
V=√Tμ
- If the velocity is halved (V' = V/2), then:
V′=√T′μ
- This means:
(V2)2=T′μ
- Therefore, if V is halved, the new tension (T') becomes:
T′=T4
- The tension in the string is directly proportional to the mass (M) placed on the pan:
T∝M
- Therefore, if the new tension is T' = T/4, then the new mass (M') that should be placed on the pan is:
M′=M4
To make the string vibrate in 2n loops with the same frequency, the mass that should be placed on the pan is:
M4
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
In Melde's experiment it was found that the string vibrated in three loops wien 8 gm were placed on the scale pan. What mass must be placed on the pan to make the string vibrate in six loops? (Neglect the mass of the string and the scale pan]
View SolutionIn Melde's experiment it was found that the string vibrated in 3 loops when 8gm were placed in a pan. What mass must be placed in the pan to make the string vibrate in 5 loops? (Neglect the mass of the string an the pan).
View Solution
Knowledge Check
When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
A1 : 1 : 1 : 1B1 : 2 : 3 : 4C4 : 3 : 2 : 1D1 : 4 : 9 : 16
In an experiment, sonometer wire vibrates in 4 loops when a 50 g weight is placed in the pan of weight 15 g. To make the wire vibrates in 6 loops the mass that has to be removed from the pan is approximately [frequency of vibration remains constant]
View SolutionA string of length 2m and mass 2 gmn is stretched by a certain tension so that it vibrates in 4 segments with a frequency of 600 Hz. What is the tension ?
View SolutionA circular ring of small thickness and of inner and outer diameters 3.8 cm and 4.2 cm respectively , suspended on one side of a common balance is exactly balanced by keeping sufficient mass in the pan on other side .At this instant the lower surface of ring is just resting on the surface of a liquid . Now if the ring is puled up gently , such that it does not loose its contact with the liquid , find how much mass should be changed in other pan , again to keep the balance in balanced position ? (Assume angle of contact is zero and surface tension of liquid is (1/π) N/m)
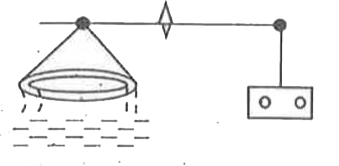
View SolutionIn Melde's experiment , when a string is stretched by a piece of glass it vibrates with 7l∞ps . When the glass piece is completely immersed in water the string vibrates in 9l∞ps. What is the specific gravity of glass ?
View SolutionIn an experiment of standing waves, a string 90cm long is attached to the prong of an electrically driven tuning fork that scillates perpendicular to the length of the string at a frequency of 60Hz. The mass of the string is 0.044kg. What tension (in newton) must the string be under (weights are attached to the other end) if it is to oscillate in four loops?
View SolutionThe string AB vibrates in two loops with a tuning fork when block hasngs in air. Now block is completely immersed in water, the string vibrates in three loops with same tuning fork. The specific gravity of block is :

View SolutionWhen block hangs in air, the horizontal string vibrates in its tenth harmonic in unison with a particular tuning fork. When block is placed in elevator acceleration in downward direction, the same string vibrates in its eleventh harmonic with same tuning fork. What will be acceleration of elevator ?
_PHY_E06_324_Q01.png)
_PHY_E06_324_Q02.png)
View Solution