Shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current I given by i=i0sinωt. Find(a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developd in the frame in the time interval 0 to 20πω.
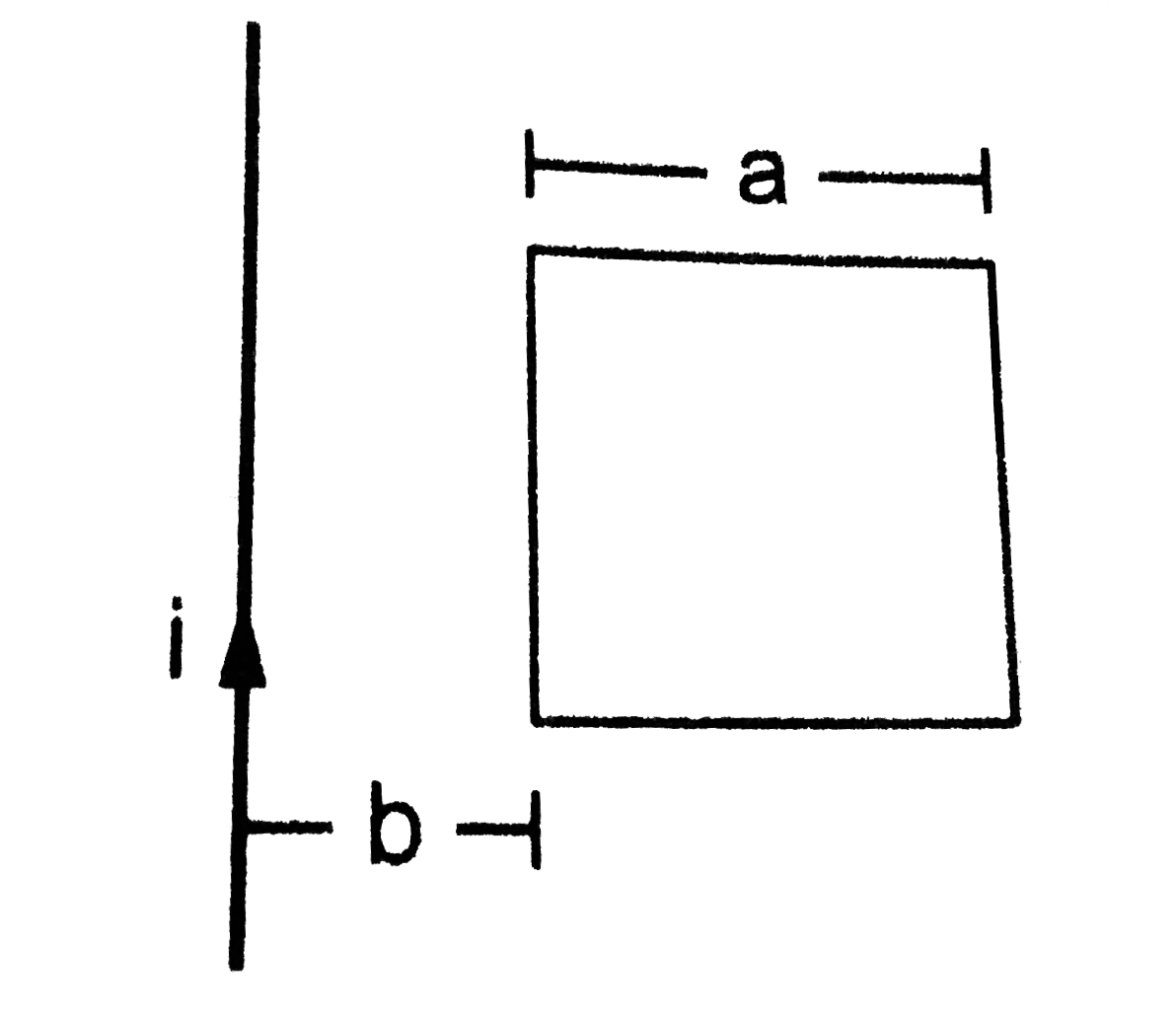
Magnetic field due to long wire at distance x
B=μ0i2πx
Taking a small area of length a and width dx
dA=adx
dϕ=BdA=μ0ia2πdxx
Total flux through the loop
ϕ=μ0ia2π∫b+abdxx=μ0ia2π|1nx|b+ab
=μ0ia2π[1n(b+a)−1n(b)]
=μ0ia2π1n(1+ab)
=μ0i0a1n(1+ab)ω2πcosωt
(d) Induced emf
e=dϕdt=μ0ia1n(1+ba)ω2πcosωt
(c) Heat developed in
t=0 to t=40πω=20T
H=∫20T0e2Rdt
=[μ(0)i0aω1n(1+ba)]24π2R∫20T0cos2ωtdt
=[μ(0)i0aω1n(1+ba)]24π2R(T2×20)
=[μ(0)i0aω1n(1+ba)]24π2R.10.2πω
=5[μ0i0a1n(1+(b)a)]2ωπR

Topper's Solved these Questions
Similar Questions
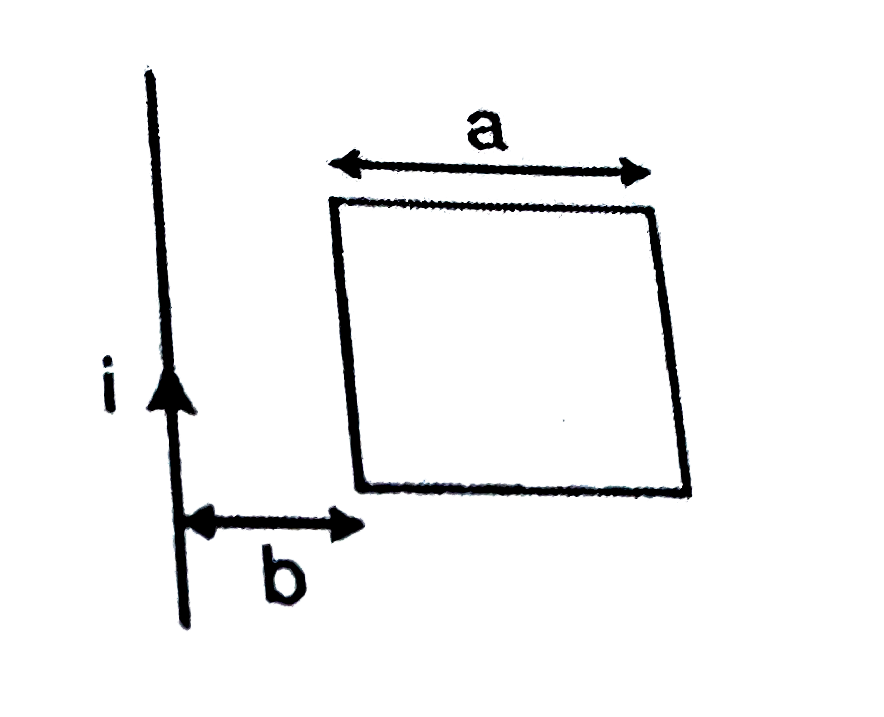
Figure shows a fixed square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i=i0cos(2πt/T). Find (a) the flux of the magnetic field through the square frame , (b) the emf induced in the frame and ( c) the heat developed in the frame in the time interal 0 to 10T.
 View Solution
View SolutionFigure showns a fixed square frame of wire having a total resistance r placed coplanarly with a long staight wire.The wire carries a current i given by i=i0cos(2πl/T).Find (a) the flux of the magnetic field through the square frame (b)the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to 10T.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
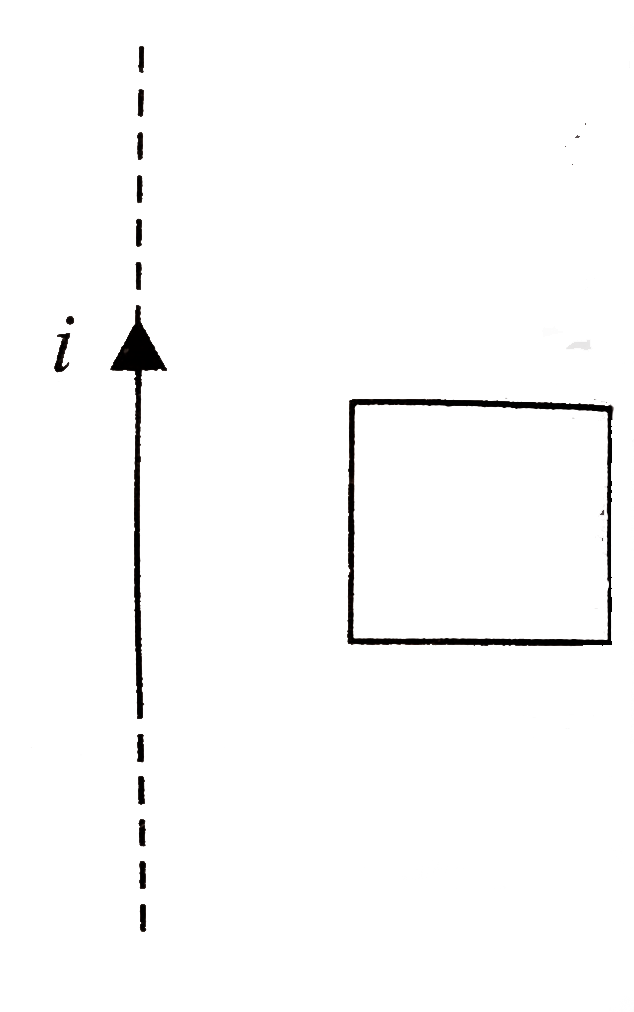 Aif didt=0, no current is induced in the loopBif didt>0 , current in the loop is clockwise.Cif didt<0 , current in the loop is anticlockwise.Dif didt>0 , current in the loop is anticlockwise.
Aif didt=0, no current is induced in the loopBif didt>0 , current in the loop is clockwise.Cif didt<0 , current in the loop is anticlockwise.Dif didt>0 , current in the loop is anticlockwise. - Question 2 - Select One
A conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
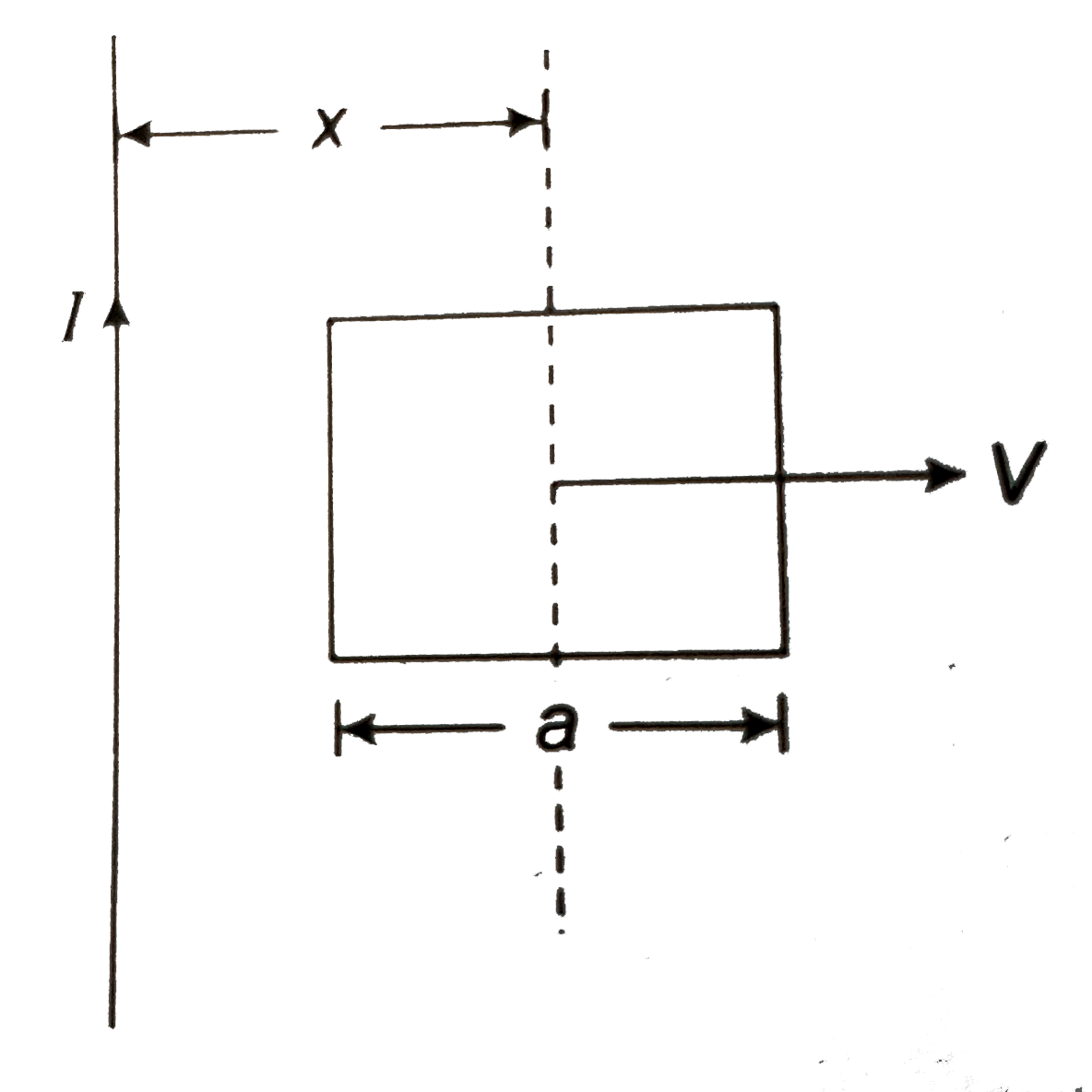 A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A wire carries an alternating current i=i0 sin omega t. In there an electric field in the vicinity of the wire?
View SolutionThe magnitude of magnetic field at a distance 'r' from a long straight wire carrying a current I is given by B = …………………… .
View SolutionIn the frame work of wires shown in figure, a current I ampere is flowing. Find the magnetic field at O.
 View Solution
View SolutionA square frame of edge 10 cm is placed with its ositivae normal making on angle of 600 with a uniform electric field of 20Vm−1. Find the flux of the electric field through the surface bounded by the frame.
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.
 View Solution
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
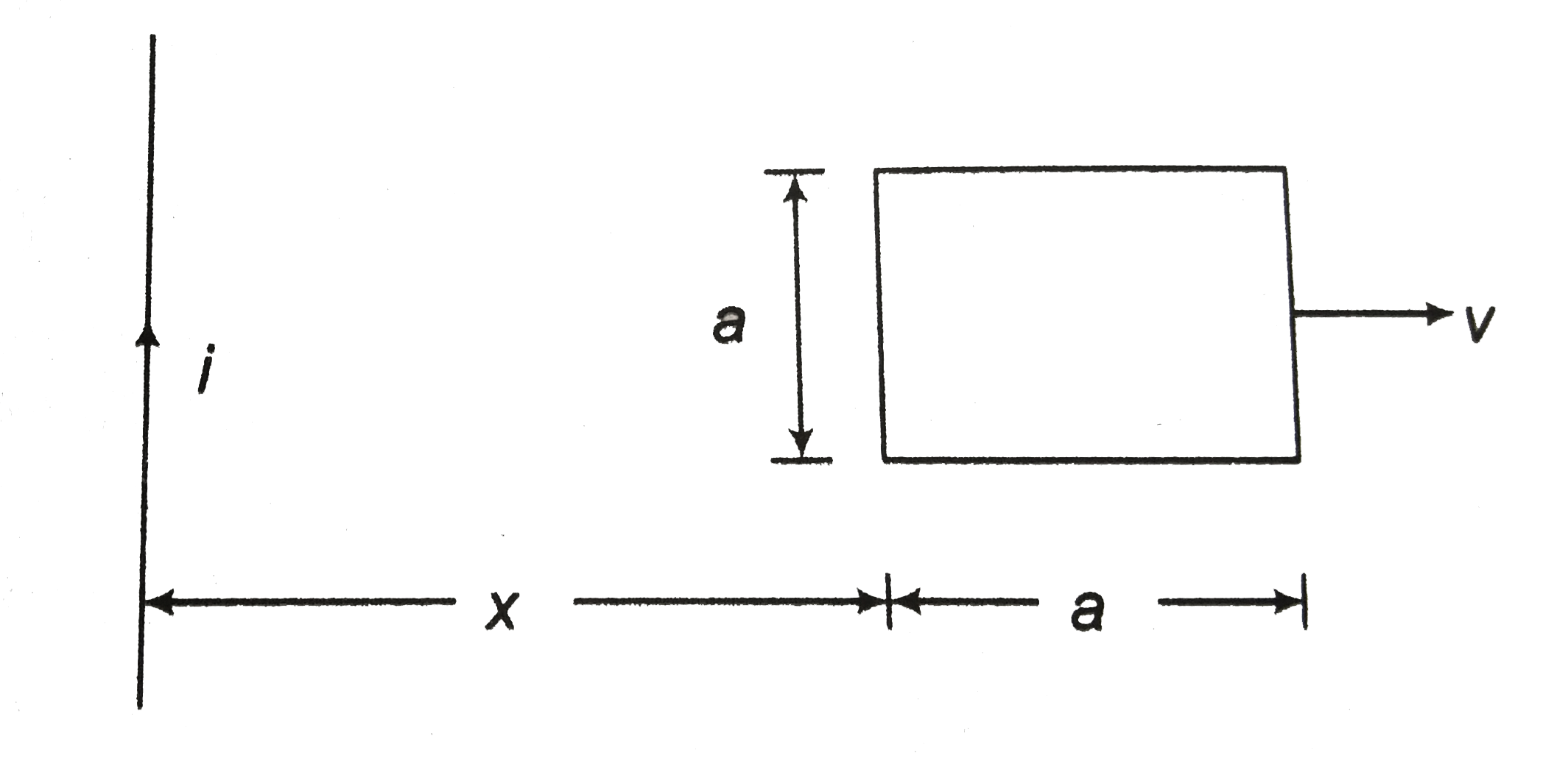 View Solution
View Solution

