A square frame of edge 10 cm is placed with its ositivae normal making on angle of 600 with a uniform electric field of 20Vm−1. Find the flux of the electric field through the surface bounded by the frame.
To find the electric flux through the surface bounded by the square frame, we will follow these steps:
Step 1: Understand the formula for electric flux
The electric flux (Φ) through a surface is given by the formula:
Φ=∫E⋅dA
For a uniform electric field, this simplifies to:
Φ=E⋅A⋅cos(θ)
where:
- E is the magnitude of the electric field,
- A is the area of the surface,
- θ is the angle between the electric field and the normal to the surface.
Step 2: Calculate the area of the square frame
The area A of a square with edge length l is given by:
A=l2
Given that the edge length l=10 cm=0.1 m:
A=(0.1 m)2=0.01 m2
Step 3: Identify the electric field and the angle
The electric field E is given as 20 V/m, and the angle θ between the electric field and the normal to the surface is 60∘.
Step 4: Calculate the cosine of the angle
We need to find cos(60∘):
cos(60∘)=12
Step 5: Substitute values into the flux formula
Now we can substitute the values into the flux formula:
Φ=E⋅A⋅cos(θ)
Substituting the known values:
Φ=20 V/m⋅0.01 m2⋅12
Step 6: Perform the calculation
Calculating the above expression:
Φ=20⋅0.01⋅0.5=0.1 V m
Final Answer
The electric flux through the surface bounded by the frame is:
Φ=0.1 V m
---
The electric flux (Φ) through a surface is given by the formula:
Φ=∫E⋅dA
For a uniform electric field, this simplifies to:
Φ=E⋅A⋅cos(θ)
where:
- E is the magnitude of the electric field,
- A is the area of the surface,
- θ is the angle between the electric field and the normal to the surface.
The area A of a square with edge length l is given by:
A=l2
Given that the edge length l=10 cm=0.1 m:
A=(0.1 m)2=0.01 m2
The electric field E is given as 20 V/m, and the angle θ between the electric field and the normal to the surface is 60∘.
We need to find cos(60∘):
cos(60∘)=12
Now we can substitute the values into the flux formula:
Φ=E⋅A⋅cos(θ)
Substituting the known values:
Φ=20 V/m⋅0.01 m2⋅12
Calculating the above expression:
Φ=20⋅0.01⋅0.5=0.1 V m
The electric flux through the surface bounded by the frame is:
Φ=0.1 V m
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Worked Out Examples
8 Videos
- GAUSS LAWBOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Short Answer
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
79 Videos
Similar Questions
A charge Q is placed at the centre of a cub. Find the flux of the electric field through the six surfaced of the cube.
View SolutionA square coil of 600 turns, each side 20cm, is placed with its plane inclined at 30∘ to a uniform magnetic field of 4.5×10−4Wbm−2, Find the flux through the coil.
View Solution
Knowledge Check
In a uniform electric field find the total flux associated with the given surfaces (R is radius )
 Aa=0,b=0,c=0Ba=0,b=(πR2E),c=0Ca=2πRE,b=(πR2E),c=0Da=πR2E,b=0,c=0
Aa=0,b=0,c=0Ba=0,b=(πR2E),c=0Ca=2πRE,b=(πR2E),c=0Da=πR2E,b=0,c=0In a uniform electric field find the total flux associated with the given surfaces (R is radius)
 Aa=0,b=0,c=0,Ba=0,b=(πR2E),c=0Ca=2πRE,b=(πR2E),c=0Da=πR2E,b=0,c=0
Aa=0,b=0,c=0,Ba=0,b=(πR2E),c=0Ca=2πRE,b=(πR2E),c=0Da=πR2E,b=0,c=0
A charge Q is placed at a distance α2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
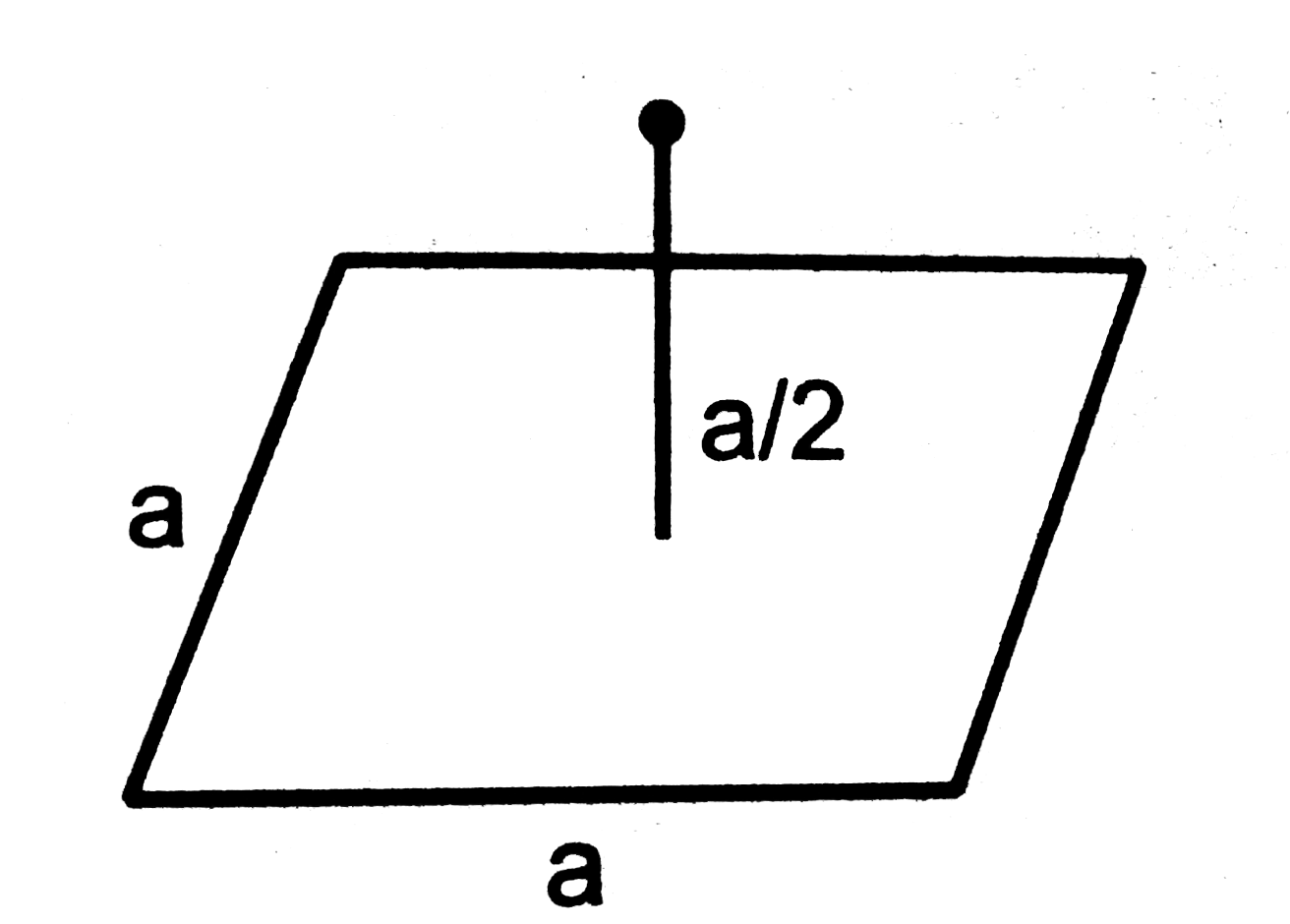
View SolutionAn electric dipole of length 4 cm, when placed with its axis making an angle of 60∘ with a uniform electric field, experiences a torque of 4√3Nm. Calculate the
a. magnitude of the electric field, and
b. potential energy of the dipole, if the dipole has charges of ±8nC.
View SolutionA rectangular surface of sides 10cmand15cm is palaced inside a uniform electric field fo 25Vm−1, such that normal to the surface makes an angle of 60∘ with the direction of electric field. Find the flux of electric field through the rectangular surface.
View SolutionA rectangular surface of sides 10cmand15cm is palaced inside a uniform electric field fo 25Vm−1, such that normal to the surface makes an angle of 60∘ with the direction of electric field. Find the flux of electric field through the rectangular surface.
View SolutionA uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.
View SolutionAn electric dipole of length 2 cm is placed with its axis making an angle of 60∘ to a uniform electric field of 105NC−1 if its experiences a torque is 8√3Nm, calculate the
(i). Magnitude of the charge on the dipole and
(ii). potential energy of the dipole.
View Solution
