Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
va
2av
2av(2+√3)
2av(2−√3)
The correct Answer is:D
d. t=av−vcosπn.Heren=12

⇒t=av−vcos(2π12)=2av(2−√3).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type26videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type35videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
six particles are situated at the corners of a regular hexagon. These particles start moving with equal speed of 10 m/s in such that velocity of any one particle is directed towards the next particle. Find the rate (in m/s) at which length of a side of the hexagon is decreasing.
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
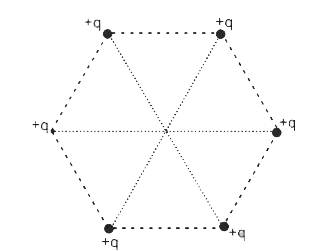 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.
AavBa2vCa3vD2a3v - Question 2 - Select One
Three particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant
 A3ms−1B5ms−1C6ms−1Dzero
A3ms−1B5ms−1C6ms−1Dzero - Question 3 - Select One
Four particles of masses 1 kg, 2 kg, 3 kg, and 4 kg are situated at the corners of a square and moving at speed 3ms−1,4ms−1,1ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particle at the next comer symmetrically. The momentum of the system at this instant is
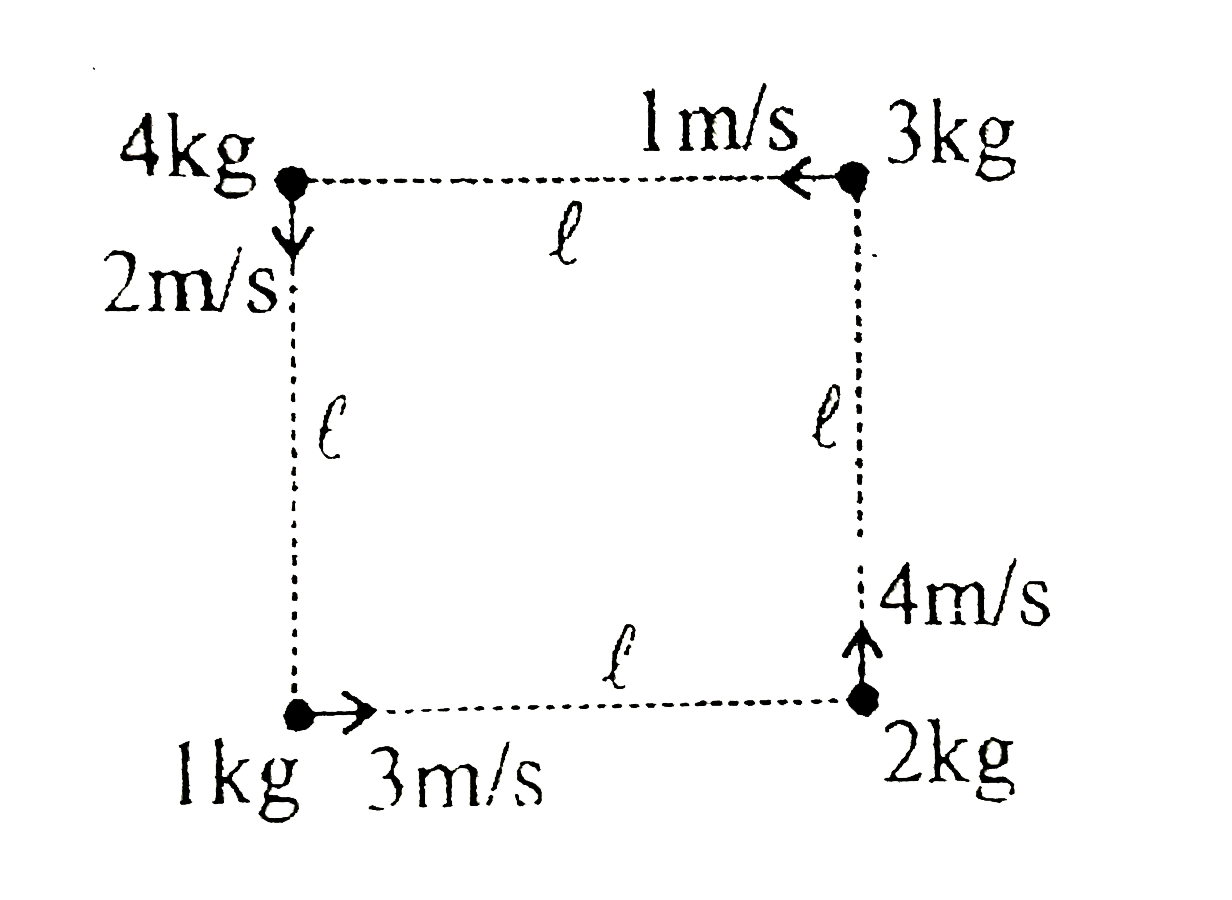 A3kgms−1B5kgms−1C6kgms−1DZero
A3kgms−1B5kgms−1C6kgms−1DZero
Four particles A,B,CandD are situated at the cornerst of a square ABCD of side aatt−0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CB~andD along DA. At what time will these particles meet each other ?
View SolutionSix identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View SolutionA particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
View Solution

