Six particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
6Gm2a2
6Gmm0a2
zero
6Gma4
The correct Answer is:C
To find the net gravitational force on the point mass m0 placed at the center of a regular hexagon with six particles of mass m at its corners, we can follow these steps:
Step 1: Understand the Configuration
We have a regular hexagon with six corners, each occupied by a particle of mass m. The point mass m0 is located at the center of the hexagon.
Step 2: Determine the Distance from the Center to Each Corner
In a regular hexagon, the distance from the center to any corner (vertex) can be calculated using the relationship:
d = \frac{a}{\sqrt{3}} \quad \text{(where a is the edge length)}
However, for gravitational force calculations, we can directly use the edge length a and the geometry of the hexagon.
Step 3: Calculate the Gravitational Force from One Corner
The gravitational force F exerted by one corner mass m on the mass m0 at the center is given by Newton's law of gravitation:
F=Gmm0d2
where G is the gravitational constant and d is the distance from the center to a corner.
Step 4: Analyze the Forces
Since the hexagon is symmetric, the forces exerted by the six corner masses on the central mass m0 will have equal magnitudes but different directions.
Step 5: Resolve the Forces into Components
Each force can be resolved into x and y components. Due to the symmetry of the hexagon:
- The forces acting in opposite directions will cancel out.
- For example, the force from mass at corner 1 will cancel with the force from mass at corner 4, and so on.
Step 6: Calculate the Net Force
Since all forces from the corner masses cancel each other out due to symmetry, the net gravitational force Fnet on the mass m0 is:
Fnet=0
Conclusion
Thus, the net gravitational force on the point mass m0 at the center of the hexagon is:
Net Gravitational Force=0
We have a regular hexagon with six corners, each occupied by a particle of mass m. The point mass m0 is located at the center of the hexagon.
In a regular hexagon, the distance from the center to any corner (vertex) can be calculated using the relationship:
d = \frac{a}{\sqrt{3}} \quad \text{(where a is the edge length)}
However, for gravitational force calculations, we can directly use the edge length a and the geometry of the hexagon.
The gravitational force F exerted by one corner mass m on the mass m0 at the center is given by Newton's law of gravitation:
F=Gmm0d2
where G is the gravitational constant and d is the distance from the center to a corner.
Since the hexagon is symmetric, the forces exerted by the six corner masses on the central mass m0 will have equal magnitudes but different directions.
Each force can be resolved into x and y components. Due to the symmetry of the hexagon:
- The forces acting in opposite directions will cancel out.
- For example, the force from mass at corner 1 will cancel with the force from mass at corner 4, and so on.
Since all forces from the corner masses cancel each other out due to symmetry, the net gravitational force Fnet on the mass m0 is:
Fnet=0
Thus, the net gravitational force on the point mass m0 at the center of the hexagon is:
Net Gravitational Force=0
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL I(C.W.)
51 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL II (C.W.)
38 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV
40 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Six equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View SolutionSix particles each of mass 'm' are placed at six verties A,B,C,D,Eand F of a regular hexagon of side 'a'. A seventh particle of mass 'M' is kept at center 'O' of the hexagon.
(a)Find net force on 'M'.
(b)Find net force on 'M' if particles at A is removed.
(c) Find net force on 'M' if particles at A and C are removed .
View Solution
Knowledge Check
Six identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
ALB6L/7CL/7DL√3Six charges are placed at the corner of a regurlar hexagon as shown . If an electron is placed at its centre O, force on it will be :
 AZeroBAlong OFCAlong OCDNone of these
AZeroBAlong OFCAlong OCDNone of theseFive identical point charges +Q are placed at the five corners of a regular hexagon of edge length a. One corner is empty. Electric field intensity at the centre of the hexagon is
AZeroBQ4πε0d2, towards the empty cornerCQ4πε0d2, away from the empty cornerD5Q4πε0a2 towards the empty corner
Six s imilar magnetic poles are placed on six corners of a regular hexagon of side 10cm. A south pole of strength 10Am is placed at the centre of hexagon. Find the magnetic force on the south pole.
View SolutionA point mass of 10 kg is placed at the centre of earth. The weight of the point mass is
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
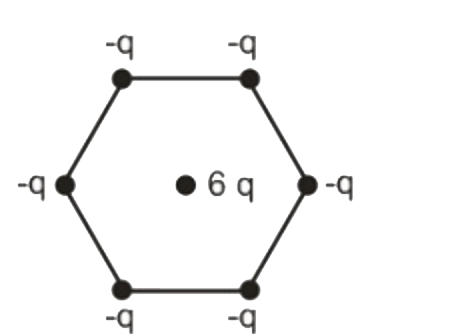
View Solution
