Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Consider the diagram below, in which six point masses are placed at six vertices A, B, C, D, E and F
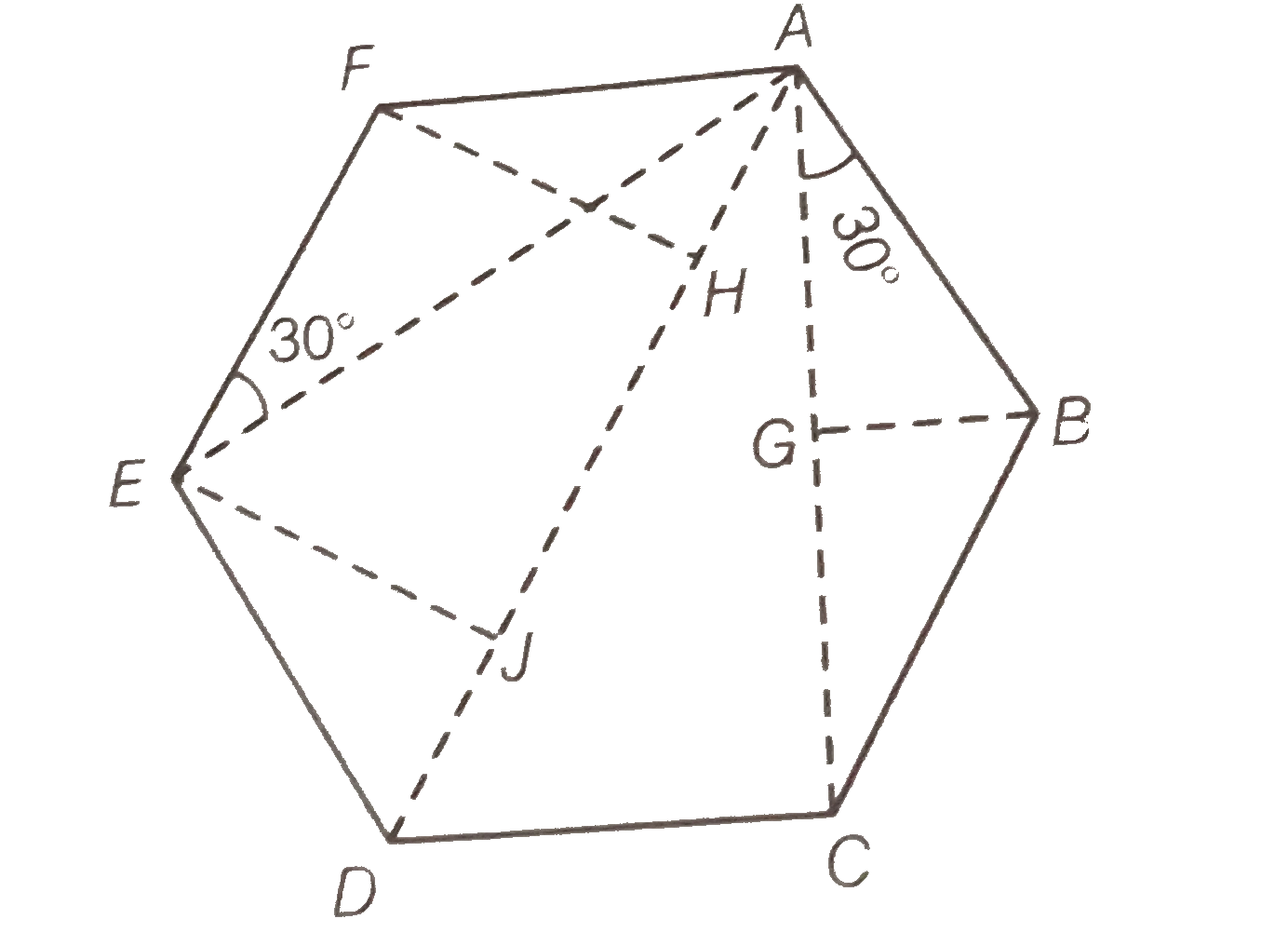
AC=AG+GC=2AG
=2lcos30∘=2l√3/2
=√3l=AE
AD=AH+HJ+JD
=lsin30∘+l+lsin302=2l
Force on mass m at A due to mass m at B is, f1=Gmml2 along AB.
Force on mass m at A due to mass m at C is, f2=Gm×m(√3l)2=Gm23l2 along AC. [∴AC=√3l]
Force on mass m at A due to mass m at D is, f3=Gm×m(2l)2=Gm24l2 along AD [∴AD=2l]
Force on mass m at A due to mass m at E is f4=Gm×m(√3l)2=Gm23l2 along AE.
f5=Gm×ml2=Gm2l2 along AF.
Resultant force due to f1 and f5 is F1=√f21+f25+2f1f5cos120∘=Gm2l2 along AD.
[∴ Angle between f1 and f5=120∘]
Resultant force due to f2 and f4 is, F2=√t22+t24+2f2f4cos60∘
=√3Gm23l2=Gm2√3l2 along AD.
So, net force along AD =F1+F2+F3=Gm2l2+Gm2√3l2+Gm24l2=Gm2l2(1+1√3+14)
Topper's Solved these Questions
Similar Questions
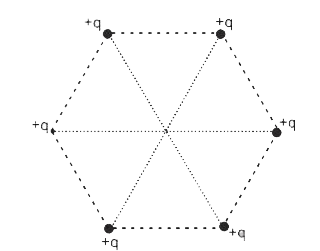
Six equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View Solution
Knowledge Check
Six identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
ALB6L/7CL/7DL√3Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
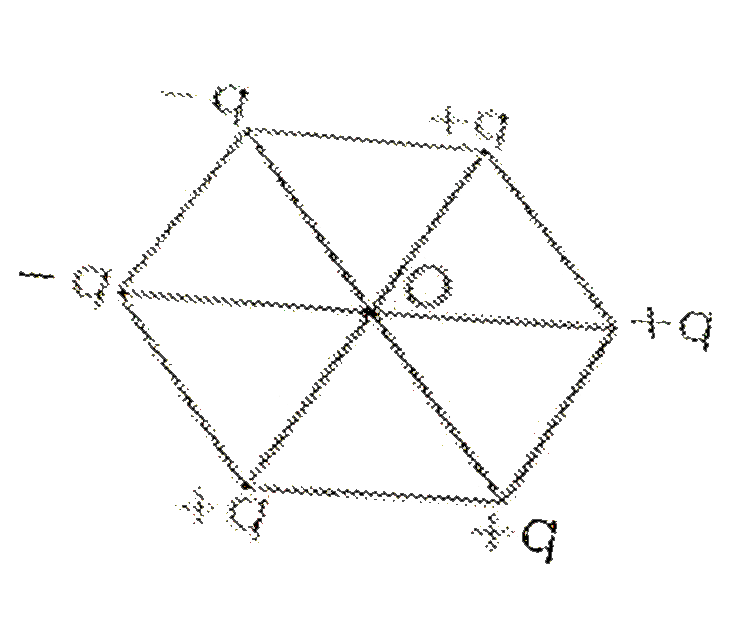
Find the magnitude of electric field at the centre of regular hexagon.Aq4πε0a2BzeroCq2πε0a2Dnone of theseFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2
Five point masses m each are kept at five vertices of a regular pentagon. Distance of centre of pentagon from any one of the verticle is 'a'. Find gravitational potential and filed strength at centre.
View SolutionFive point charges each of charges +q are placed of five vertices of a regular hexagon of side 'l'. Find the magnitude of the resultant force on a charge -q placed at the centre of the hexagon.
(##U_LIK_SP_PHY_XII_C01_E09_018_Q01.png" width="80%">
View SolutionFour masses, each equal to M are placed at the four corners of a square of side a. Calculate the force of attraction on another mass m, kept at the centre of the square.
View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
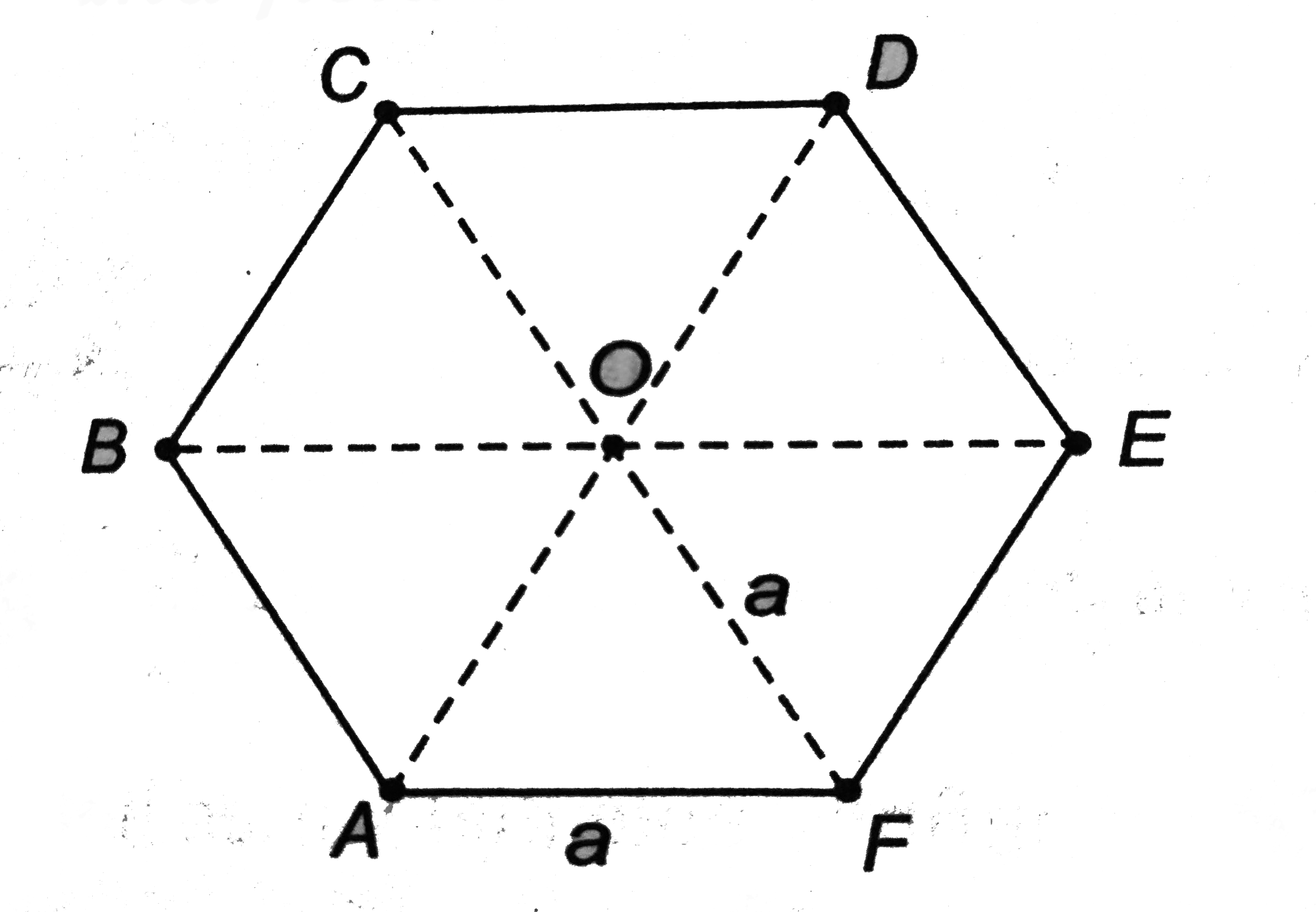 .
.
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View Solution
