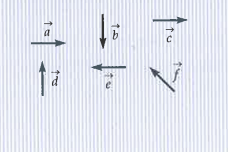
Six vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?
The correct Answer is:(c )
Step by step video, text & image solution for Six vector vec(a) through vec(f) have the magnitudes and direction indicated in the figure. Which of the following statements is true? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Multiple choice
10 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Fill in the blanks
10 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Multiple choice
10 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
Knowledge Check
Six vectors ˆa to ˆi have the magnitude and directions indicated in the figure . Which of the following statement is true ?
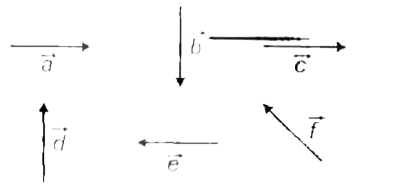 A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→f
A→b+→e=→fB→b+→c=→fC→d+→c=→fD→d+→e=→fIf →P×→Q=→R, then which of the following statements is not true?
A→R⊥→PB→R⊥→QC→R⊥(→P+→Q)D→R⊥(→P×→Q)If →A,→B,→C are mutually perpendicular vectors then which of the following statements is wrong?
A→C×(→A×→B)=0B→A×→B∣∣→A×→B∣∣=→C∣∣→C∣∣C→A.→B=→B.→C=→C.→A=0D(→B+→C) is perpendicular to →A
Consider the following statements:
1. The magnitude of →a×→b is same as the area of a triangle with sides →aand→b.
2. If →a×→b=→0 where →a≠0.→b≠0 then →a=λ→b which of the following statements is/are correct?
View SolutionTwo vector →A and →B have equal magnitudes. Then the vector →A+→B is perpendicular :
View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionThree coplanar vectrors →A,→B and →C have magnitudes 4,3 and 2 respectively. If the angle any two vector is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2

View Solution→A is a vector with magnitude A, then the unit vector ˆA in the direction →A is
View Solution