Three coplanar vectrors $\to A, \to B$ and $\to C$ have magnitudes $4, 3$ and $2$ respectively. If the angle any two vector is $120^{\circ}$ then which of the following vector may be equal to $\frac{3 \to A}{4} + \frac{\to B}{3} + \frac{\to C}{2}$

A

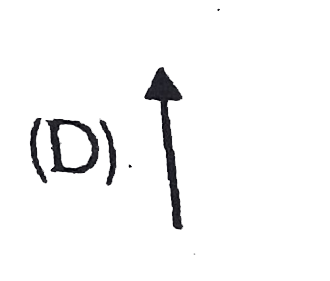
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

As $∣ ∣ ∣ \frac{\to B}{3} ∣ ∣ ∣ = ∣ ∣ ∣ \frac{\to C}{2} ∣ ∣ ∣$ so $\frac{\to B}{3} + \frac{\to C}{2} = - \frac{\to A}{4}$ therefore $\frac{3 \to A}{4} + \frac{\to B}{3} + \frac{\to C}{2} = \frac{\to A}{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The magnitudes of vectors $\to A, \to B and \to C$ are 3,4 and 5 unit respectively. If $\to A + \to B = \to C,$ the angle between $\to A and \to B$ is
A $\frac{π}{2}$
B ${cos}^{- 1} (0.6)$
C ${tan}^{- 1} (\frac{7}{5})$
D $\frac{π}{4}$
Question 2 - Select One
The magnitude of vectors $\to A, \to B and \to C$ are 3, 4 and 5 units respectively. If $\to A + \to B = \to C$ , the angle between $\to A and \to B$ is
A $\frac{π}{2}$
B $\frac{π}{4}$
C ${tan}^{- 1} (\frac{7}{5})$
D ${cos}^{- 1} (0.6)$
Question 3 - Select One
If magnitudes of vectors $\to A, \to B$ and $\to C$ are 5, 4 and 3 units respectively and, $\to A = \to B + \to C$ then angle between $\to A$ and $\to B$ is
A ${cos}^{- 1} (\frac{3}{5})$
B ${cos}^{- 1} (\frac{4}{5})$
C ${sin}^{- 1} (\frac{4}{5})$
D ${tan}^{- 1} (\frac{3}{5})$

ALLEN-MISCELLANEOUS-SUBJECTIVE QUESTION

Home
Ask Doubt
Profile