Sketch the variation of electric circle potential on the x-axis with respect to x for x=−∞ to x=+∞ in the following cases.
(a) 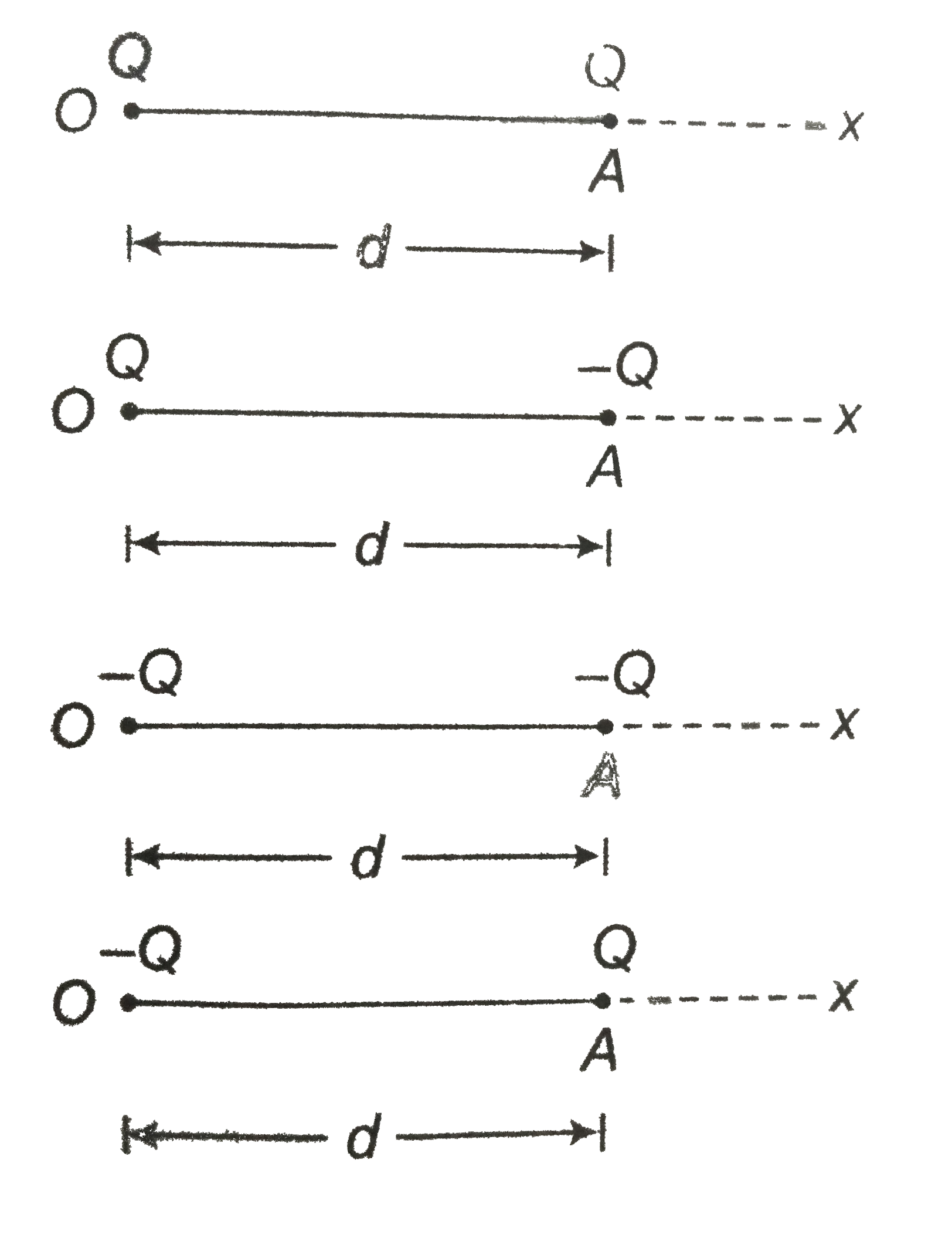
(a) Electric potential at P :
Vp=14π∈0.[Qx+Qd−x]=Q4π∈0.dx(d−x)
Vp is minimum if x(d−x) is maximum.
x(d−x) is maximum if x=d−x⇒x=d/2.
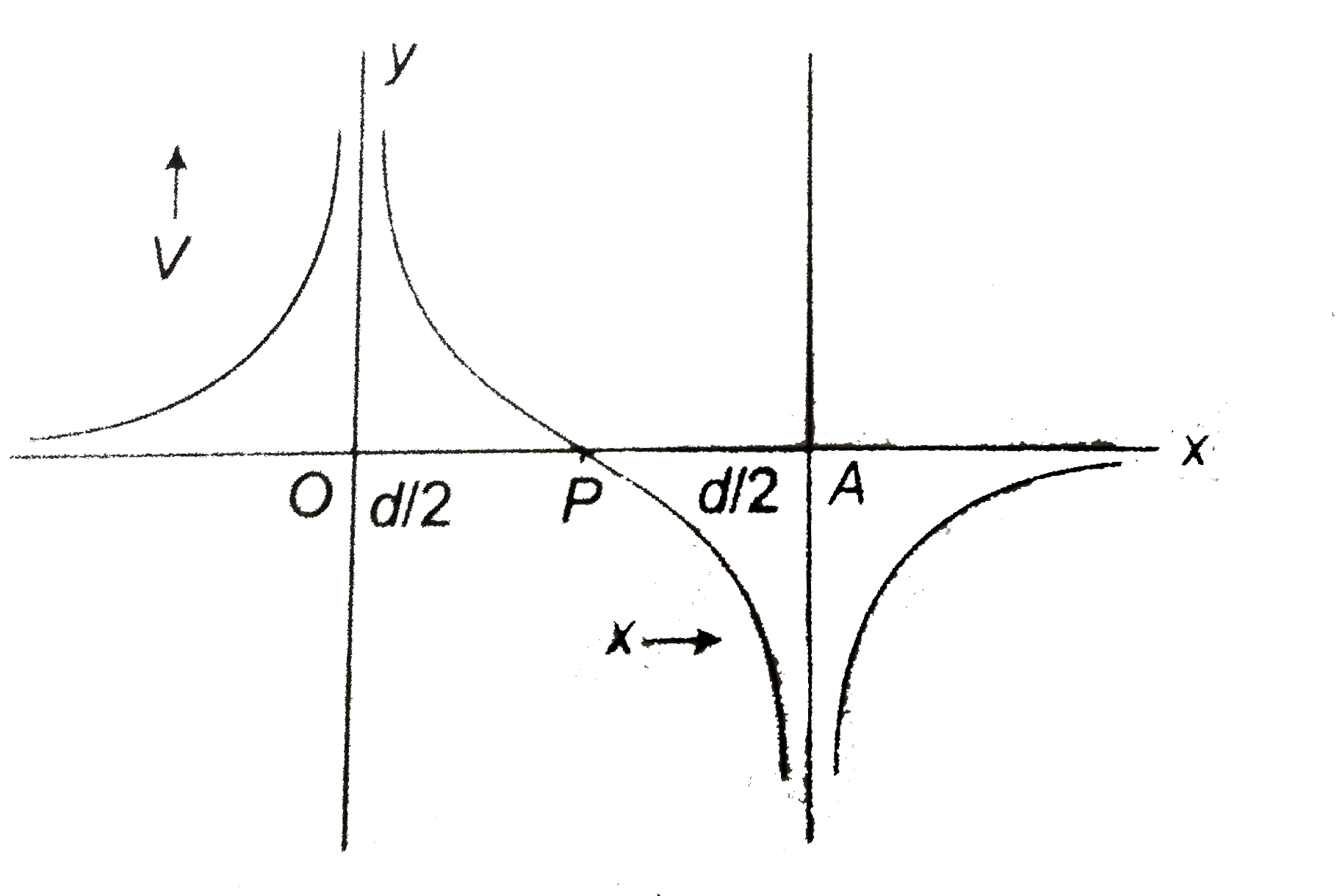
At mid -point of OA , electric potential is minimum.
At O:x→0,V→∞
At A:x→d,V→∞
From O to A , electric potential decreases reaching to minimum value and then increases.
Left of O : At distance x from O
V=14π∈0[Qx+Qd+x]
x→0,V→∞
x→−∞,V→0
Right of A : At distance x from O
V=14π∈0[Qx+Qx−d]
x→d,V→∞
x→∞,V→0
(B) At mid - point of OA,V=0
0<x<d2,Vis+ve
d2<x<d,Vis−ve
x→0,V→∞
x→0,V→∞
x→−∞,V→0
Right of A:Vis−ve
x→d,V→∞
x→∞,V→0
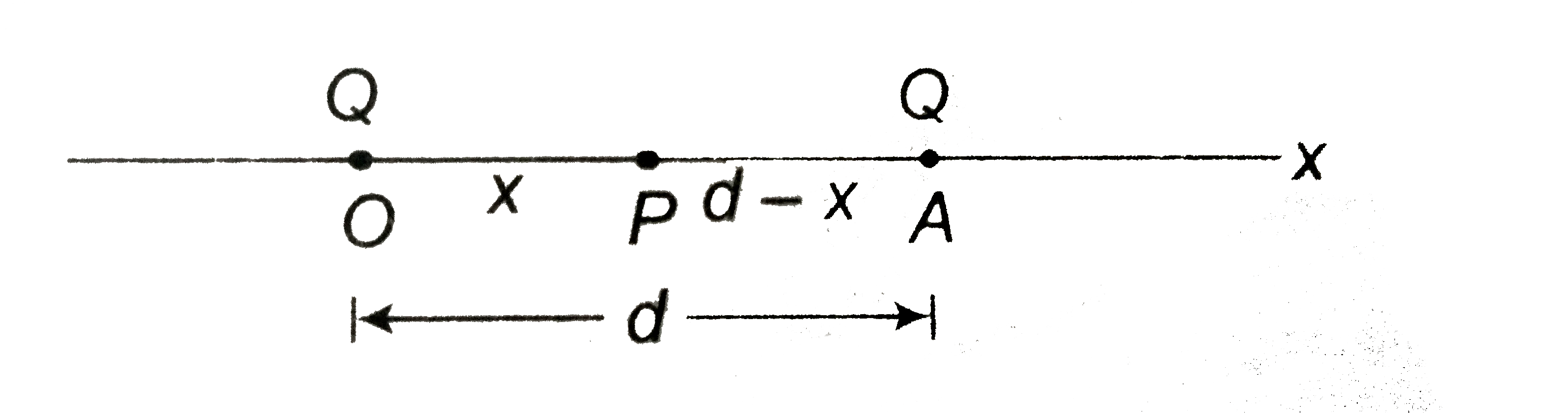

Topper's Solved these Questions
Similar Questions
Sketch the vairation of electric potential on the x-axis with respect to x for x=−∞ to x=+∞ in the following cases

View SolutionThe variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
 .
.
View Solution
Knowledge Check
A charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
A(a) 0B(b) q8πε0x0ln2C(c) ∞D(d) qln24πε0x0A particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
AAt point away from the origin, the particle is in unstable equilibriumBFor any finite non-zero value of x, there is a force directed away from the originCIf its total mechanical energy is k/2, it has its minimum kinetic energy at the originDFor small displacements from x = 0, the motion is simple harmonicRange of f(x)=x2+x+2x2+x+1−∞<x<∞, is
A[1,∞]B[1,∞)C[1,75)D(1,73]
The variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
 .
.
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View Solution(a) The charges each Q are placed at x−d,2d,4d,…∞. Find electric potential at origin O.
(b) A charge +Q is placed at each of the points x=d,x=3d,x=5d,…..,∞ on the x-axis , and a charge −Q is placed at each of the points x=2d,x=4d,x=6d,...,∞.Find the electric potential at the origin O.
View Solution(a) The charges each Q are placed at x−d,2d,4d,…∞. Find electric potential at origin O.
(b) A charge +Q is placed at each of the points x=d,x=3d,x=5d,…..,∞ on the x-axis , and a charge −Q is placed at each of the points x=2d,x=4d,x=6d,...,∞.Find the electric potential at the origin O.
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View Solution
