Some gas at 300K is enclosed in a container. Now the container is placed on a fast moving train. While the train is in motion, the temperature of the gas
rises above 300 K
falls below 300 K
remains unchanged
becomes unsteady
The correct Answer is:C
To solve the problem regarding the behavior of gas temperature when its container is placed on a fast-moving train, we can follow these steps:
1. Understanding the Initial Conditions:
- The gas is initially at a temperature of 300 K.
- The container is placed on a fast-moving train.
2. Analyzing the Effect of Train Motion:
- The train moves with a certain velocity (V). However, the gas inside the container is not directly affected by the train's velocity in terms of temperature.
3. Temperature Dependence:
- The temperature of a gas is related to the average kinetic energy of its molecules. The formula for the root mean square (RMS) speed of gas molecules is given by:
Vrm=√3RTm
- Here, R is the gas constant, T is the temperature in Kelvin, and m is the mass of the gas molecules.
4. Velocity of the Container:
- Since the container is moving with the train, its velocity does not change the average kinetic energy of the gas molecules inside it. The gas molecules are still in thermal equilibrium with each other.
5. Conclusion on Temperature:
- The temperature of the gas remains unchanged at 300 K while the train is in motion. This is because the temperature of the gas is dependent on the kinetic energy of the gas molecules, which is not affected by the external motion of the container.
Final Answer:
The temperature of the gas remains at 300 K while the container is on the fast-moving train.
---
- The gas is initially at a temperature of 300 K.
- The container is placed on a fast-moving train.
- The train moves with a certain velocity (V). However, the gas inside the container is not directly affected by the train's velocity in terms of temperature.
- The temperature of a gas is related to the average kinetic energy of its molecules. The formula for the root mean square (RMS) speed of gas molecules is given by:
Vrm=√3RTm
- Here, R is the gas constant, T is the temperature in Kelvin, and m is the mass of the gas molecules.
- Since the container is moving with the train, its velocity does not change the average kinetic energy of the gas molecules inside it. The gas molecules are still in thermal equilibrium with each other.
- The temperature of the gas remains unchanged at 300 K while the train is in motion. This is because the temperature of the gas is dependent on the kinetic energy of the gas molecules, which is not affected by the external motion of the container.
The temperature of the gas remains at 300 K while the container is on the fast-moving train.
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - A Tacking it together
55 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.2
20 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
Two cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View Solution
Knowledge Check
Cooking gas container are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will
AincreaseBdecreaseCremains the sameDdecrease for some and increase for others
Two moles of a diatomic gas at 300 K are kept in a nonconducting container enclosed by a piston . Gas is now compressed to increase the temperature from 300 K to 400 K. Find word done by the gas

View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionIf a gas container is placed in a moving train, the temperature of gas will increase.
Kinetic energy of gas molecules will increase.
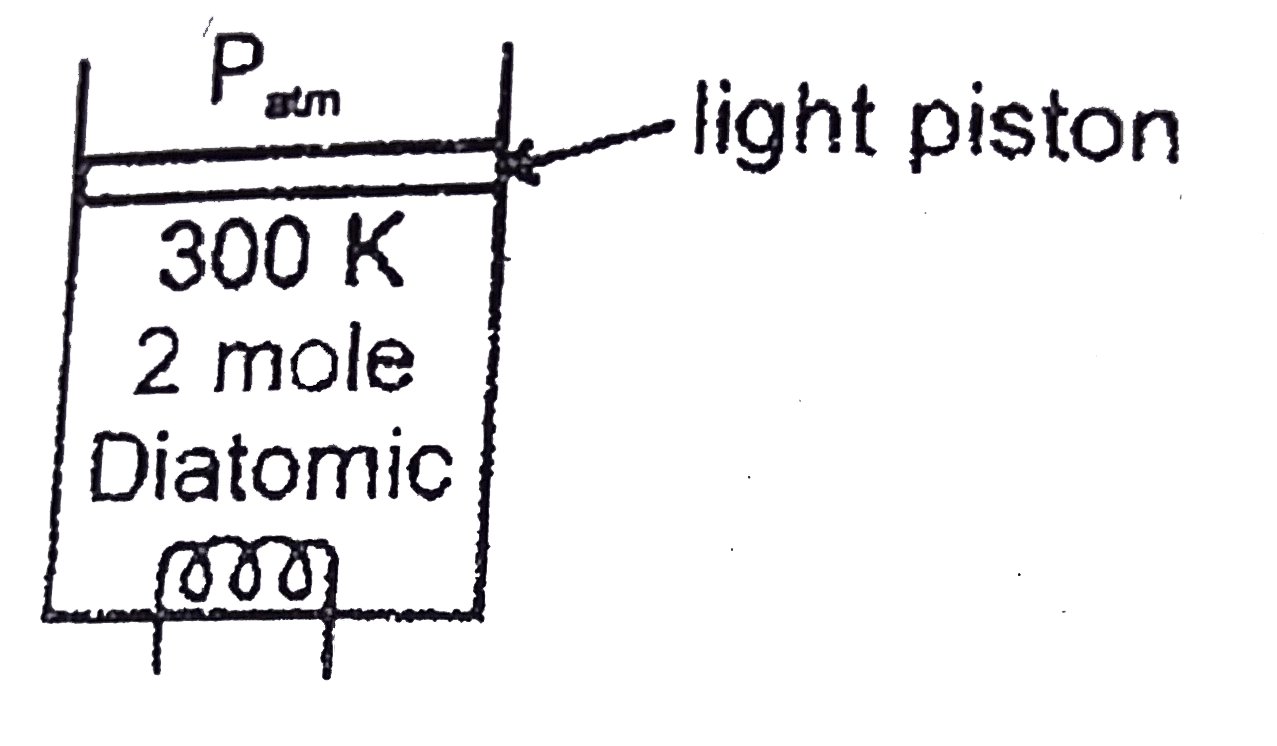
View SolutionTwo moles of a diatomic gas at 300K are enclosed in a cylinder as shown in figure. Piston is light. Find out the heat given if the gas is slowly heated to 400K in the following three cases.
(i) Piston to free to move
(ii) If piston does not move
(iii) If piston is heavy and movable
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View SolutionA cylinder fitted with a piston contains an ideal monoatomic gas at a temperature of 400K. The piston is held fixed while heat ΔQ is given to the gas, it is found the temperature of the gas has increased by 20K. In an isobaric process the same ΔQ heat is supplied slowely to it. Find the change in temperature in the second process?
View SolutionIf the critical temperature of a gas is 300 K then the ratio of its inversion and Boyle's temperature will be
View Solution