Sphere A of mass 'm' moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
1−e1+e
1+e1−e
e+1)e−1
e−1e+1
The correct Answer is:B
From conservation of linear momentum:
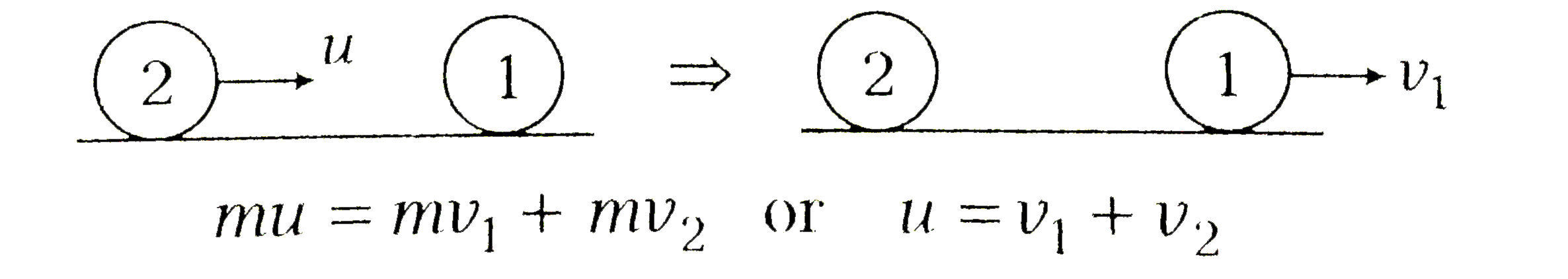
From definition of e,
v1−v2=eu..............(ii)
Solving these two equations, we get
v1=1+e2u and v2=1−e2u
∴ ⎛⎜⎝v1v2=1+e1−e
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A sphere of mass m moving with a uniform velocity v hits another identical sphere at rest. If the coefficient of restitution is e, the ratio of the velocities of the two sphere after the collision is e−1e+1.
View SolutionA particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is
View Solution
Knowledge Check
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and of coefficient of restitution (e). The ratio of velocities of the two spheres, after collision, will be
Ae(e+1)B(1−e1+e)C1eD(e+1e)A sphere of mass m moving with a constant velocity hits another stationary sphere of the same mass, if e is the coefficient of restitution, then ratio of speed of the first sphere to the speed of the second sphere after collision will be
A(1−e1+e)B(1+e1−e)C(e+1e−1)D(e−1e+1)A sphere of mass m moving with a velocity u hits another stationary sphere of same mass. If e is the coefficient of restitution, what is the ratio of the velocities of two spheres after the collision?
A1BeC1+e1−eD2−e1+e
A particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View SolutionA sphere of mass m moving with constant velocity u, collides with another stationary sphere of same mass. If e is the coefficient of restitution, the ratio of the final velocities of the first and second sphere is
View SolutionA body of mass m moving with a constant velocity collides head on with another stationary body of same mass if the coefficient of restitution between the bodies is 12 then ratio of velocities of two bodies after collision with be
View SolutionA ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
View Solution
