A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is

A

$\frac{2 u M}{M}$

B

$(2 u \frac{M}{M})$

C

$2 \frac{u}{1 + \frac{m}{M}}$

D

$(2 \frac{u}{1 + \frac{M}{m}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

If target is at rest, then final velocity of bodies are

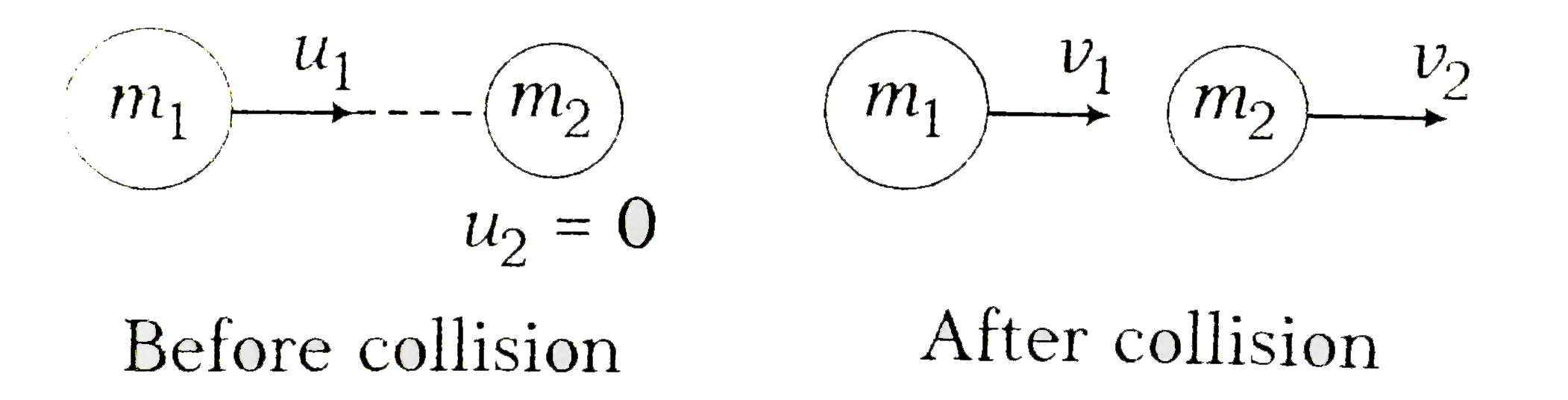
$v_{1} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} u_{1}$ ...................(i)
and $v_{2} = \frac{2 m_{1} u_{1}}{m_{1} + m_{2}}$ .................(ii)
From eqs (i) and (ii), $\frac{v_{1}}{v_{2}} = \frac{m_{1} - m_{2}}{2 m_{1}} = \frac{2}{5} \Rightarrow \frac{m_{1}}{m_{2}} = 5$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
Av
B $v \sqrt{5}$
C $\frac{2}{\sqrt{3}} v$
D $\frac{v}{\sqrt{3}}$
Question 2 - Select One
A body of mass $M$ moves with velocity $v$ and collides elasticity with another body of mass $m (M > > m)$ at rest , then the velocity of the body of mass $m$ is
Av
B2v
C $v / 2$
DZero
Question 3 - Select One
A body of mass $M$ moves with velocity $v$ and collides elasticity with another body of mass $m (M > > m)$ at rest , then the velocity of the body of mass $m$ is
A $v$
B $2 v$
C $v / 2$
DZero

DC PANDEY-CENTRE OF MASS-Check points

Home
Ask Doubt
Profile