Springs of constants k, 2k, 4k, 8k,…….,2048k are connected in series. A mass m is attached to one end and the system is allowed to oscillate. The time period is approximately
2π√m2k
2π√2mk
2π√m4k
2π√4mk
The correct Answer is:B
To solve the problem of finding the time period of a mass attached to a series of springs with varying spring constants, we can follow these steps:
1. Identify the Spring Constants:
The spring constants given are k,2k,4k,8k,…,2048k. This is a geometric series where the first term a=k and the common ratio r=2.
2. Determine the Number of Springs:
The last spring constant is 2048k. Since 2048=211, the series of spring constants goes from k (which is 20k) to 2048k (which is 211k). Therefore, there are 12 springs in total.
3. Calculate the Equivalent Spring Constant for Series Connection:
For springs in series, the equivalent spring constant keq is given by:
1keq=1k+12k+14k+…+12048k
This can be rewritten as:
1keq=1k(1+12+14+…+12048)
4. Sum the Series:
The series 1+12+14+…+12048 is a geometric series with:
- First term a=1
- Common ratio r=12
- Number of terms n=12
The sum Sn of a geometric series is given by:
Sn=a1−rn1−r
Substituting the values:
S12=1⋅1−(12)121−12=1−1409612=2(1−14096)≈2
(Neglecting the small term 14096)
5. Substituting Back to Find keq:
Now substituting back:
1keq=1k⋅2⟹keq=k2
6. Calculate the Time Period:
The time period T of a mass-spring system is given by:
T=2π√mkeq
Substituting keq:
T=2π√mk2=2π√2mk=2√2π√mk
Final Answer:
The time period T is approximately 2√2π√mk.
---
The spring constants given are k,2k,4k,8k,…,2048k. This is a geometric series where the first term a=k and the common ratio r=2.
The last spring constant is 2048k. Since 2048=211, the series of spring constants goes from k (which is 20k) to 2048k (which is 211k). Therefore, there are 12 springs in total.
For springs in series, the equivalent spring constant keq is given by:
1keq=1k+12k+14k+…+12048k
This can be rewritten as:
1keq=1k(1+12+14+…+12048)
The series 1+12+14+…+12048 is a geometric series with:
- First term a=1
- Common ratio r=12
- Number of terms n=12
Sn=a1−rn1−r
Substituting the values:
S12=1⋅1−(12)121−12=1−1409612=2(1−14096)≈2
(Neglecting the small term 14096)
Now substituting back:
1keq=1k⋅2⟹keq=k2
The time period T of a mass-spring system is given by:
T=2π√mkeq
Substituting keq:
T=2π√mk2=2π√2mk=2√2π√mk
The time period T is approximately 2√2π√mk.
Topper's Solved these Questions
Similar Questions
Springs of spring constants k, 2k, 4k, 8k, …… are connected in series. A mass m kg is attached to the lower end of the last spring and the systemm is allowed to vibrate. What is the time period of oscillations? Given m=40gm,k=2.0Ncm−1.
View SolutionSprings of apring constants k,2k,4k,8k . . . Are connected in series. A mass m kg is attached to the lower end of the last spring and the system is allowed to vibrate. What is the time period of oscillations?
View Solution
Knowledge Check
Springs of spring constant K,3K,9K,27K,….243K are connected in series. A mass M is attached to the last spring and the system is allowed to make oscillation. The time period will be
A2π√MKB2π√3M2KC4π9√91M3KD2π√4M3KInfinite springs with force constants k,2k,4k,8k,….. respectively are connected in series to which mass 'm' is attched. The frequency of small oscillations is……..
Af=12π√2KmBf=12π√KmCf=12π√K2mDf=12π√2048KmTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
Springs of spring constant k, 2k, 4k , 8k, …. Are connected in series. A block of mass 50 kg is attached to the lower end of the last spring and the system is set into oscillation. If k = 3.0 N/cm, what is the time period of oscillations ?
View SolutionInfinite spring with force constants k,2k,4k,8k,……..respectively are connected in series. Calculate the effetive force constant of the spring.
View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
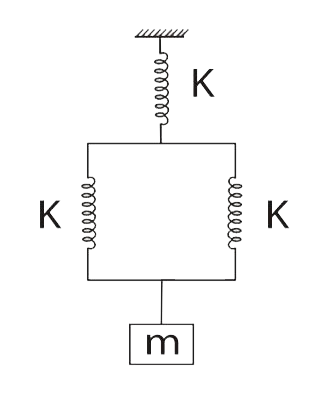
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
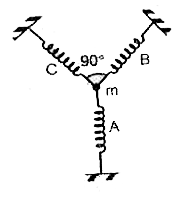
View Solution
