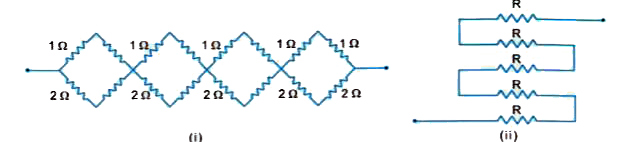
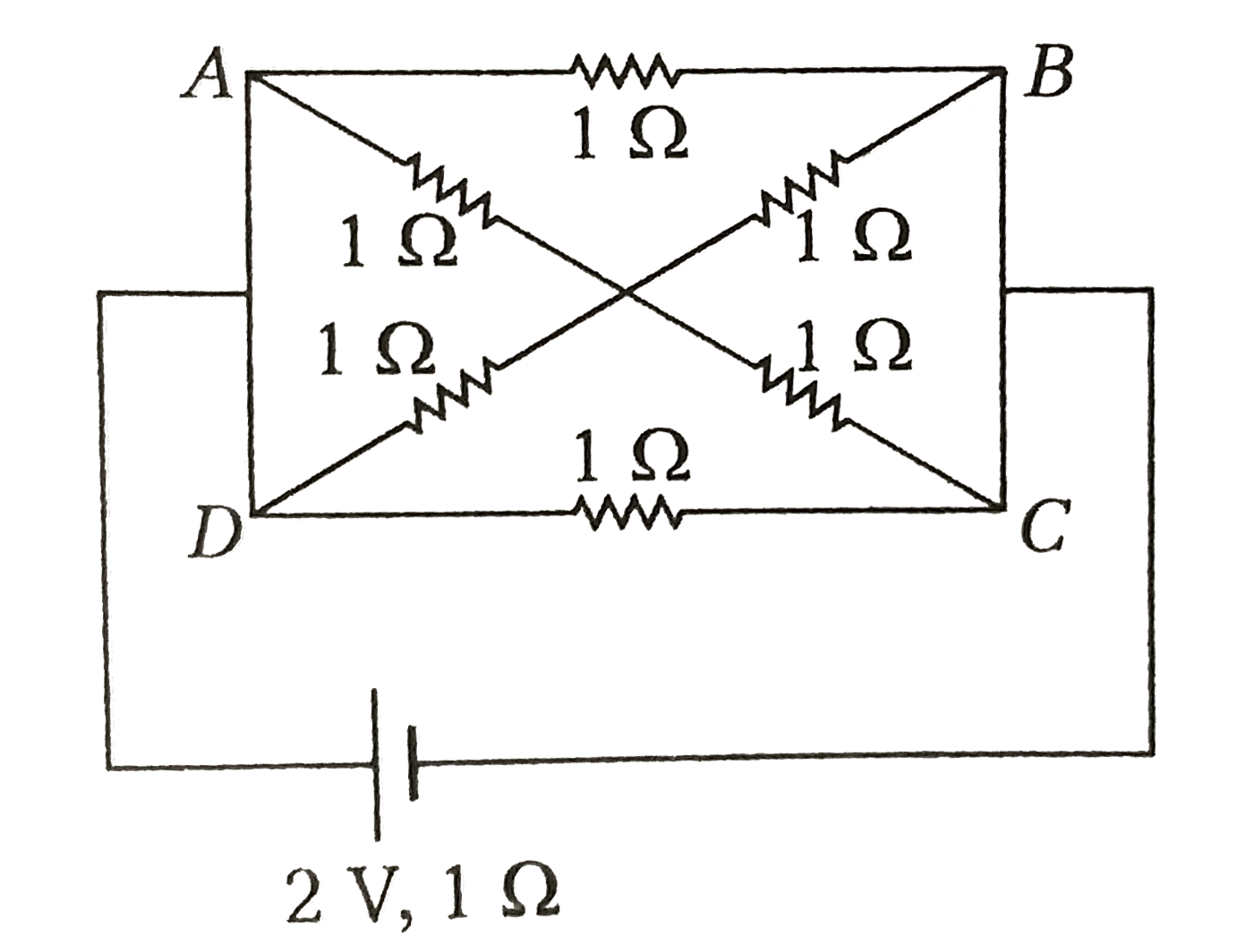
State kirchhoff's (i) junction rule and (ii) loop rule . Determine the equivalent resistance of the network given below and the total current going out of the battery . Given , each resistance has reistance of 1Ω .
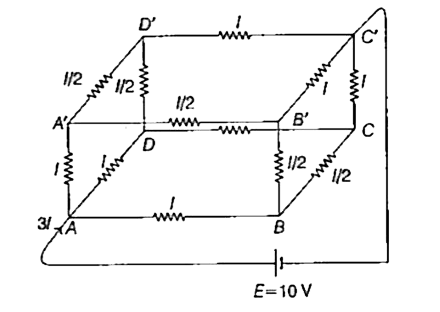
Refer to the text on page 90 (Kirchhoff.s laws) .
Let 3 l be the current through the cell Since . The path AA.,AD and AB are symmetrically placed , current through each of them is same i.e., At the junctions A,B and D the incoming current l splits equally into two outgoing branches , current through each branch will be l2 according to the figure given in question . At the junction B,C,D these current reunite and the current along B.C.D.C and CC are l each .
The total current at junction C is 3l .
Again , applying kirchhoff.s second law to the loop ABCC.EA , we get
−IR−l2R−IR+e=0⇒e=52IR
Where , R = resistance of each edge ,
and e = emf of the battery .
∴ The equivalent resistance of the networks is
R=Total emfTotal current =5IR2×3l=56R
But given , R=1Ω
∴ R=56Ω
Total current in the network is ,
3l=εR=1056=10×65=12A
⇒ l=123=4A
Similar Questions
Knowledge Check
The equivalent resistance between the point P and Q in the network given here is eqyal to (given r=32Ω)
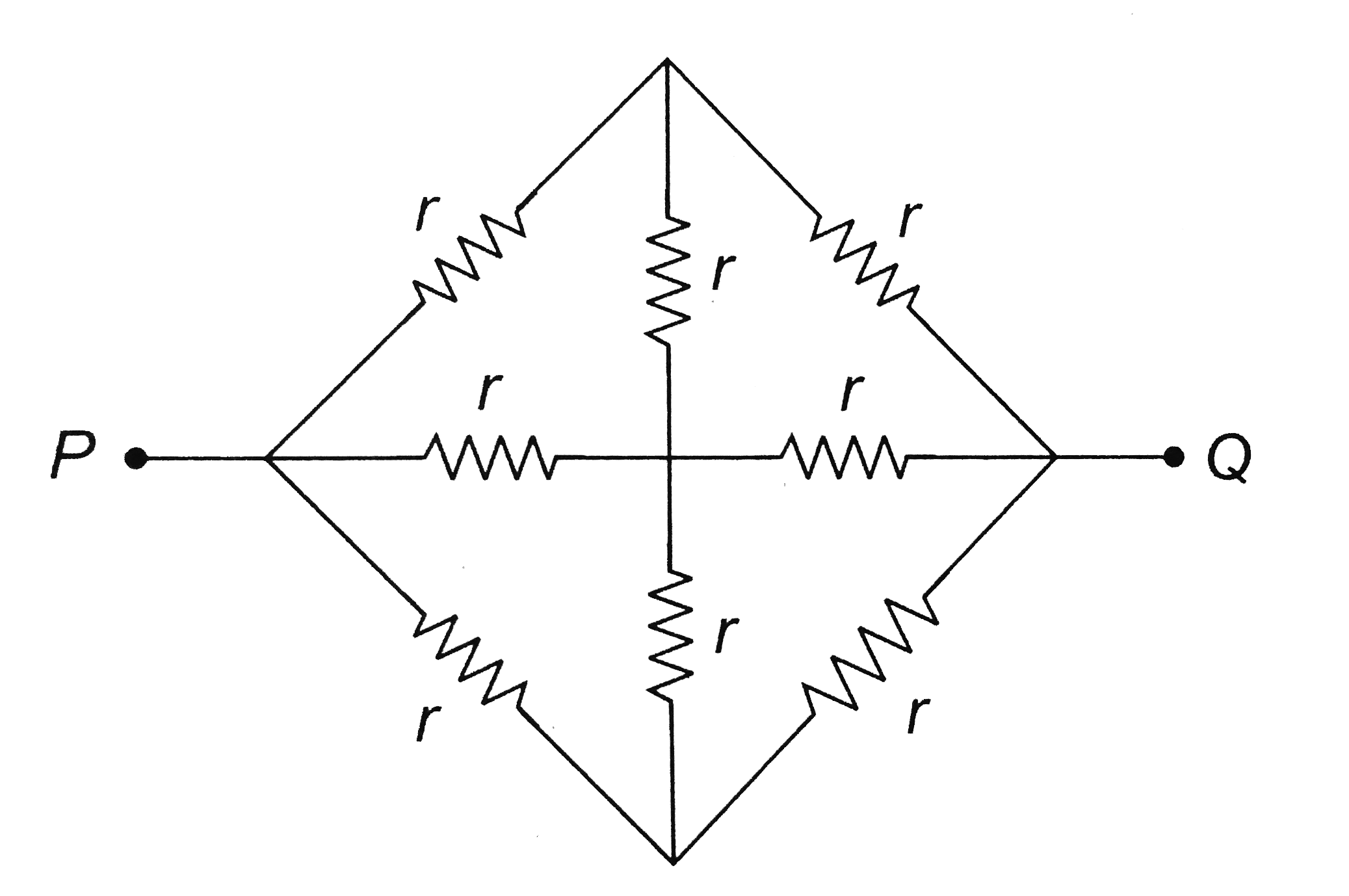 A12ΩB1ΩC32ΩD2Ω
A12ΩB1ΩC32ΩD2Ω
The equivalent resistance between points A and B of the circuit given below is …………Ω

View SolutionThe equivalent resistance between points A and B of the circuit given below is …………Ω

View SolutionDetermine the current supplied by the battery in the circuit as shown
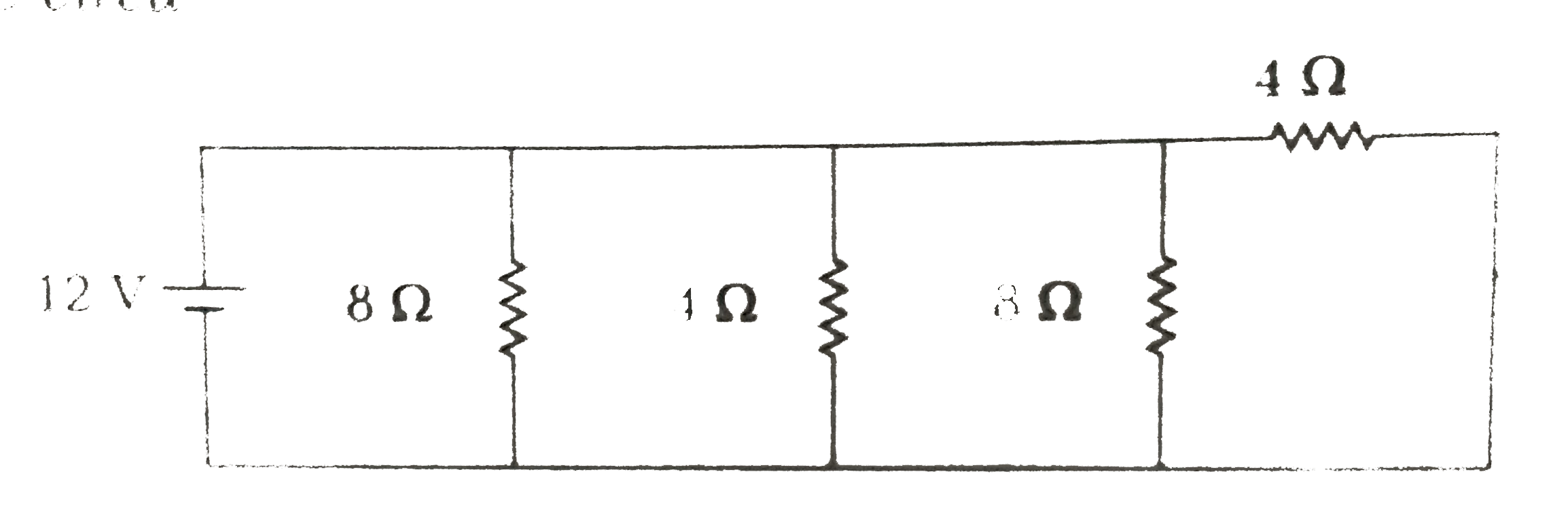
(ii) Find currents in resistance 2Ω and 4Ω.

View SolutionThe equivalent resistance between the point P and Q in the network given here is equal to (given r=32Ω)

View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
View Solution