State the condition for constructive interference.
To state the condition for constructive interference, we can break it down into the following steps:
Step 1: Understand Interference
Interference occurs when two or more waves overlap and combine to form a new wave pattern. This can result in regions of increased amplitude (constructive interference) or decreased amplitude (destructive interference).
Step 2: Define Path Difference
The path difference is the difference in the distance traveled by two waves arriving at the same point. For constructive interference to occur, this path difference must meet specific criteria.
Step 3: Condition for Constructive Interference
The condition for constructive interference can be expressed in two ways:
1. Path Difference Condition: The path difference (Δx) between the two waves must be an even multiple of the wavelength (λ). Mathematically, this can be represented as:
Δx=nλ(n=0,1,2,3,…)
where n is an integer.
2. Phase Difference Condition: The phase difference (Δφ) between the two waves must be an integer multiple of 2π. This can be expressed as:
Δϕ=2nπ(n=0,1,2,3,…)
Step 4: Conclusion
Thus, for constructive interference to occur, the path difference must be an even multiple of the wavelength, or equivalently, the phase difference must be an integer multiple of 2π.
---
Interference occurs when two or more waves overlap and combine to form a new wave pattern. This can result in regions of increased amplitude (constructive interference) or decreased amplitude (destructive interference).
The path difference is the difference in the distance traveled by two waves arriving at the same point. For constructive interference to occur, this path difference must meet specific criteria.
The condition for constructive interference can be expressed in two ways:
1. Path Difference Condition: The path difference (Δx) between the two waves must be an even multiple of the wavelength (λ). Mathematically, this can be represented as:
Δx=nλ(n=0,1,2,3,…)
where n is an integer.
Δϕ=2nπ(n=0,1,2,3,…)
Thus, for constructive interference to occur, the path difference must be an even multiple of the wavelength, or equivalently, the phase difference must be an integer multiple of 2π.
Topper's Solved these Questions
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
46 Videos
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - LONG ANSWER TYPE QUESTIONS
18 Videos
- MODEL TEST PAPER - 2BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)
4 Videos
- PRINCIPLES OF COMMUNICATIONBOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions
19 Videos
Similar Questions
The figure shows a modified Young's double slit experimental set-up.
Here SS2−SS1=λ/4.
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
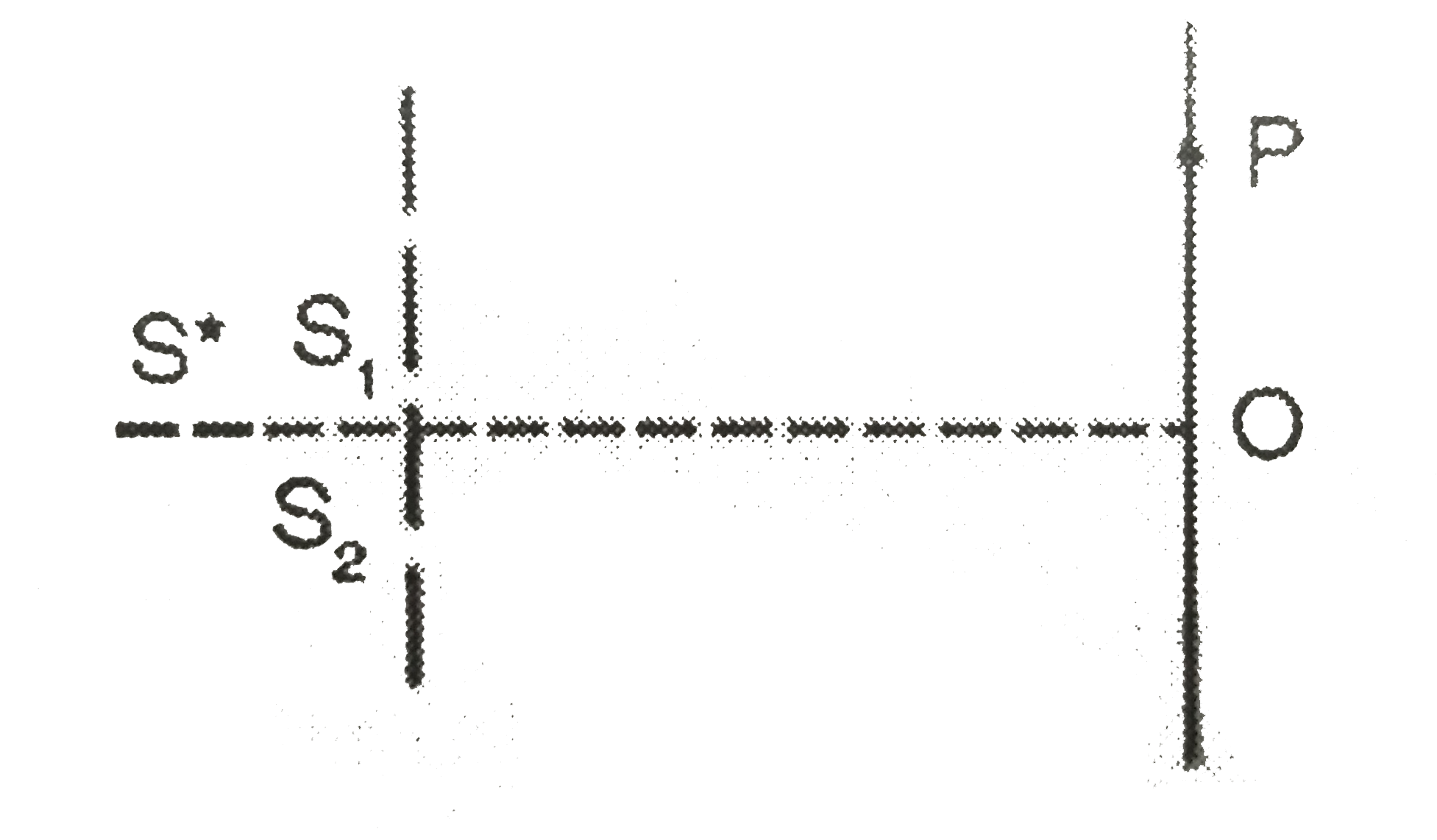
View SolutionThe figure shows a modified Young’s double slit experimental set-up. Here SS2−SS1=λ/4.
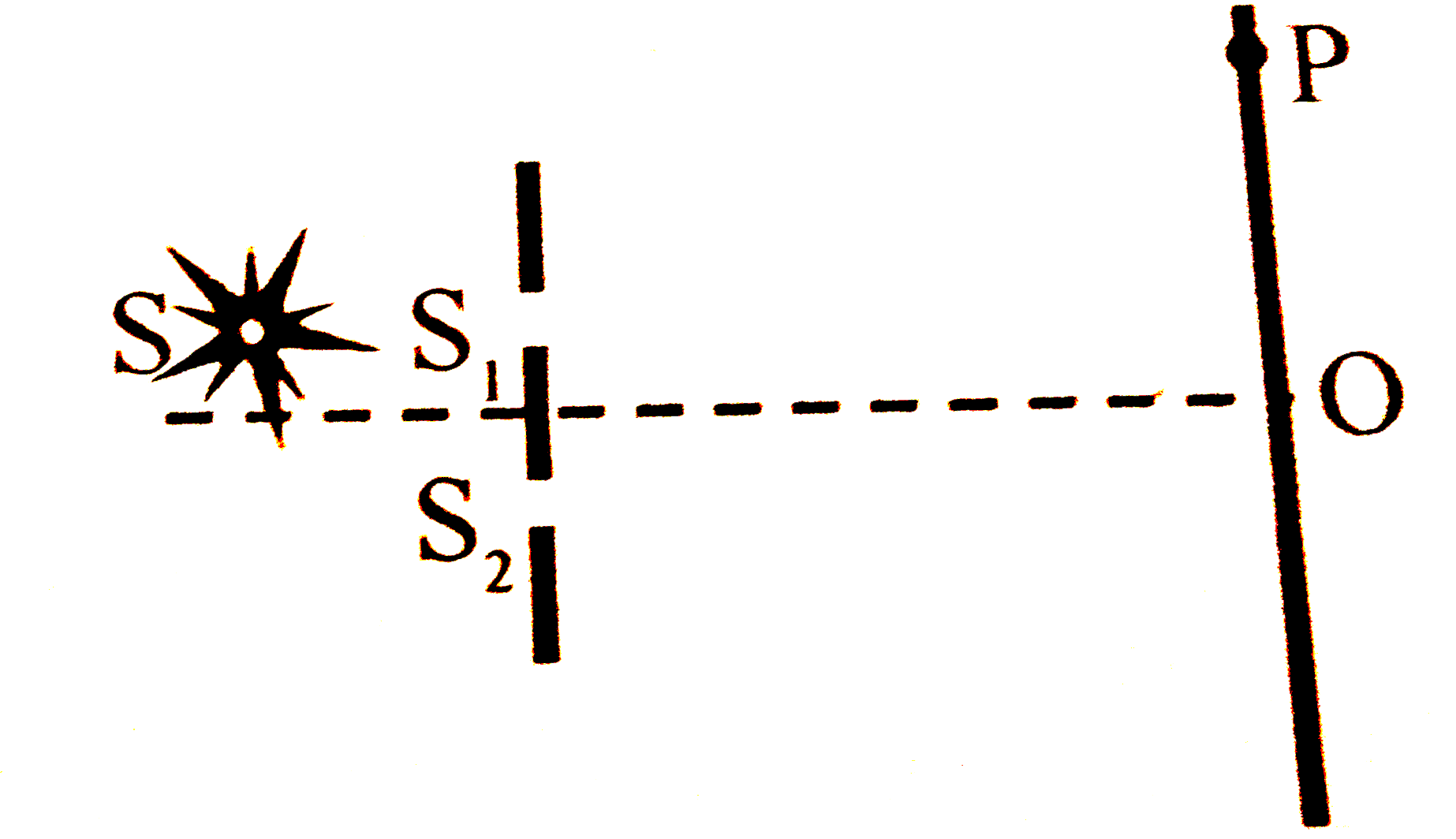
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
View Solution
Knowledge Check
Interference is an important property of light. In the given table, Column I shows the properties of interfering waves, Column II shows the phase difference, and Column III shows the path difference between two interfering waves

What are the conditions for constructive interference?A(I) (iv) (M)B(IV) (ii) (L)C(II) (i) (K)D(II) (i) (K)The amplitude of two interfering waves are a and 2a respectively. The resultant amplitude in the condition of constructive interference will be:
AaB2aC3aD5aAssertion : Energy is created in constructive interference and energy is destroyed in destructive interference.
Reason : There is maximum intensity at the point of constructive interference.AIf both assertion and reason are correct and reason is a correct explanation of the assertion.BIf both assertion and reason and correct but reason is not the correct explanation of assertion.CIf assertion is correct but reason is incorrect.DIf assertion is incorrect but reason is correct.
(a) In Young's double-slit experiment, derive the condition for
(i) constructive interference and (ii) destructive interference ata point on the screen.
(b) A beam of light consisting of two wavelenths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double-slit experiment on a screen placed 1.4m away. if the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
View Solution(a) In Young's double slit experiment, derive the condition for (i) constructive interference and (ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference frings in a Young's double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
View SolutionMonochromatic light waves of constant phase difference ϕ and amplitues A1andA2 produce an interference pattern. State an expression for the resultant amplitude at a point in the pattern. Hence deduce the conditions for (i) constructive interference with maximum intensity (ii) destructive interference with minimum intensity. Also show that the ratio of the maximum and minimum intensities
ImaxImin=(A1+A2A1−A2)2.
View SolutionThe condition for constructive interference at a point is that…………..between two waves reaching the point should be………….or……………of full wavelength.
View SolutionState the conditions for constructive and destructive inter-ference of light.
View Solution
