Statement I: In a small segament of string caruing sinusoidal wave, total energy is conserved.
Statement II: Every small part moves in SHM and in SHM total energy is conserved.
Both 'A' and 'R' are true and 'R' is the correct, explanation of 'A'.
Both 'A' and 'R' are true and 'R' is not the correct explanation of 'A'
A' is true and 'R' is false
Both 'A' and 'R' are false
The correct Answer is:D
Step by step video & image solution for Statement I: In a small segament of string caruing sinusoidal wave, total energy is conserved. Statement II: Every small part moves in SHM and in SHM total energy is conserved. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-II (Wave Equations & Basics :)
19 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-II (Strings (Speed of a travelling wave:))
23 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Matching )
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
Similar Questions
Assertion: In a small segment of string carrying sinusoidal wave, total energy is conserved.
Reason: Every small part moves in SHM and total energy of SHM is conserved.
View SolutionAssertion: In a small segment of string carrying sinusoidal wave, total energy is conserved.
Reason: Every small part moves in SHM and total energy of SHM is conserved.
View SolutionStatement-1: kinetic energy of SHM at mean position is equal to potential energy at ends for a particle moving in SHM.
Statement-2: Total energy in SHM is conserved.
View SolutionStatement I: If the amplitude of a simple harmonic oscillator is doubled, its total energy becomes four times.
Statement II: The total energy is directly proportional to the square of the smplitude of vibration of the harmonic oscillator.
View SolutionStatement-1:In a nuclear reaction energy is released , if total binding energy is increasing.
Statement-2:For a stability of a nucleus, total binding energy is more important than binding energy per nucleon.
Statement-3:Nuclear force is different for different nucleons and it dependent on charge .
View SolutionStatement-1 : Standing wave of small amplitude is generated on a string. The kinetic energy of any small section of string will be same as its potential energy.
Statement-2 : A standing wave can be written as superposition of two travelling waes. For a wave of small amplitude travelling on string, kinetic energy of any string element is equal to its potential energy at any instant.
View SolutionThere is always some loss of energy in conversion from one form of energy to another form, so the total energy is not conserved. True/False.
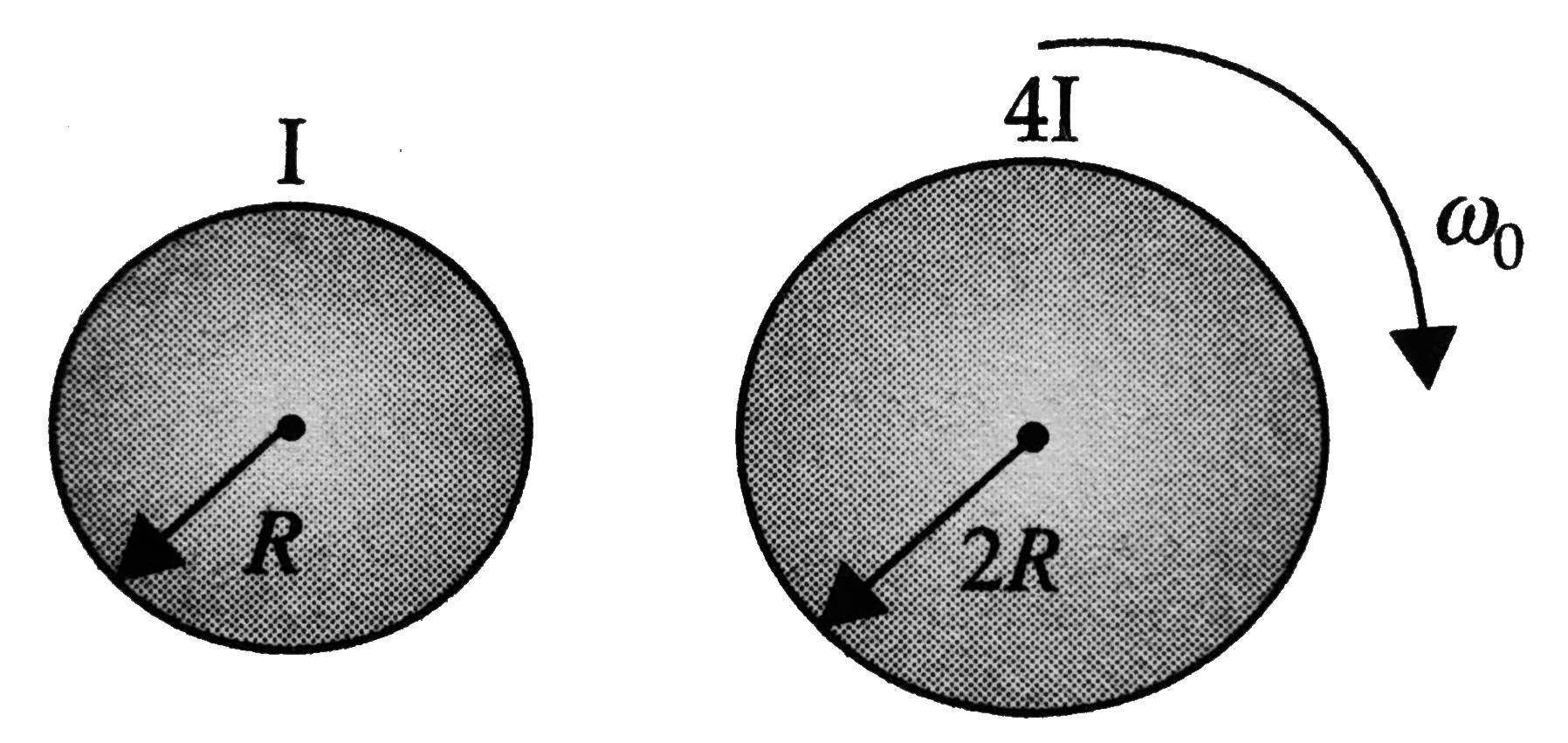
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
View SolutionThe total energy of particle performing SHM depend on : -
View SolutionStatement I : Electrical conductivity of semiconductors increases with rise in temperature.
Statement II : There is a small energy gap between conduction band and valence band.
View Solution
