Statement I: In calculating the disturbance produced by a pair of superimposed incoherent wave trians, you can add their intensities.
Statement II: I1+I2+2√I1I2cosδ. The average value of cosδ=0 for incoherent waves.
Statement I is True, statement II is True, Statement II is a correct explanation for Statement I.
Statement I is Ture, Statement II is Ture, Statement II is NOT a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:a
To solve the given problem, we need to analyze both statements provided and determine their validity in the context of wave optics, specifically regarding incoherent waves.
1. Understanding Statement I:
- Statement I claims that when calculating the disturbance produced by a pair of superimposed incoherent wave trains, their intensities can be added.
- Incoherent waves do not have a fixed phase relationship, which means they do not interfere constructively or destructively in a predictable manner.
- For incoherent waves, the resultant intensity I is simply the sum of the individual intensities I1 and I2.
- Therefore, this statement is true.
2. Understanding Statement II:
- Statement II provides the formula for the resultant intensity of two superimposed waves:
I=I1+I2+2√I1I2cosδ
- Here, δ represents the phase difference between the two waves.
- For incoherent waves, the average value of cosδ is 0 because the phase difference varies randomly.
- Thus, when averaging over time or many cycles, the term 2√I1I2cosδ contributes nothing to the average intensity, leading to:
I=I1+I2
- Therefore, this statement is also true.
3. Conclusion:
- Since both statements are true, and Statement II explains why Statement I is true, we conclude that:
- Statement I is true.
- Statement II is true.
- Statement II is the correct explanation for Statement I.
Final Answer:
Both statements are true, and Statement II is the correct explanation for Statement I.
- Statement I claims that when calculating the disturbance produced by a pair of superimposed incoherent wave trains, their intensities can be added.
- Incoherent waves do not have a fixed phase relationship, which means they do not interfere constructively or destructively in a predictable manner.
- For incoherent waves, the resultant intensity I is simply the sum of the individual intensities I1 and I2.
- Therefore, this statement is true.
- Statement II provides the formula for the resultant intensity of two superimposed waves:
I=I1+I2+2√I1I2cosδ
- Here, δ represents the phase difference between the two waves.
- For incoherent waves, the average value of cosδ is 0 because the phase difference varies randomly.
- Thus, when averaging over time or many cycles, the term 2√I1I2cosδ contributes nothing to the average intensity, leading to:
I=I1+I2
- Therefore, this statement is also true.
- Since both statements are true, and Statement II explains why Statement I is true, we conclude that:
- Statement I is true.
- Statement II is true.
- Statement II is the correct explanation for Statement I.
Both statements are true, and Statement II is the correct explanation for Statement I.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Linked Comprehension88videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
Statement I: While calculating intensities in interference pattern, we can add the intensities of the individual waves.
Statement II: Principle of superposition is valid for liner waves.View SolutionDepedence is disturbances due to two waves on time is shown in the figure, The ratio of their intensities I1/I2 be :-
_E01_012_Q01.png) .View Solution
.View SolutionDependence of disturbances due to two waves on time is shown in the figure. The ratio of their intensities I1/I2 will be
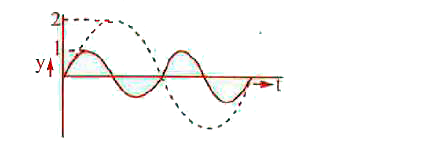 View Solution
View SolutionThe maximum intensities produced by two coherent waves of intensity I1 and I2 will be:
View SolutionStatement-1: I2+I→I3 in above reaction I2 is Lewis base and
Statement-2: Electron pair acceptor is Lewis base.View SolutionIn a triangle ABC I1,I2,I3 are excentre of triangle then show that II1.II2.II3=16R2r.
View SolutionCO+I2O5(s)→CO2+I2
View SolutionStatement I The maximum value of sinθ+cosθ is 2.
Statement II The maximum value of sinθ is 1 and that of cosθ is also 1.View SolutionCalculate the values of currents ·I1I2I3andI4 Is and loin the section of networks shown in the figure
 View Solution
View SolutionFind the maxinum intensity in case of interference of n identical waves each of intensity I0 if the interference is
(a) coherent and (b) incoherent.View Solution

