Statement I: Thin films such as soap bubble or a thin layer of oit on watar show beautiful colors when illuminated by white light.
Statement II: It happens due to the interference of light reflected form the upper surface of thin film.
(a) If both the assertion and reason are true and reason explains the assertion assertion.
(b) If both assertion and reason are true but reason does not explain the assertion
(c) If assertion is true but reason is false.
(d) If assertion is false but reason is true.
The correct Answer is:C
When a thin film of oil spreads over the surface of water is seen in broad-day light, brilliant colours are seen in the film. A similar colour pattern is seen in soap bubbles. These colours arise due to interference of sun-light reflected from the upper and lower surfaces of the film

Topper's Solved these Questions
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - AIIMS Questions
25 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
Assertion (A) : Thin films such as soap bubble or a thin layer of oil on water show beautiful colours when illuminated by white light.
Reason (R ): The colours are obtained by dispersion of lightAA is true and R is true and R is the correct explanation of A.BA and R are true but R is not correct explanation of ACA is true, R is falseDA is false, R is true.The colours seen in the reflected white light from a thin oil film are due to
ADiffractionBInterferenceCPolarisationDDispersionStatement -1: If an exceedingly thin soap film is seen in reflected light, it may appear dark
Statement -2 : Three is a phase difference of π from the rays reflected from front and rear faces of the film.AStatement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-2BStatement-1 is true, statement-2 is true, statement-2 is NOT a correct explanation for statement-1CStatement-1 is true, statement-2 is falseDStatement-1 is false, statement-2 is true
_E01_090_Q01.png)
Thin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted.
* When incident light, reaches the surface at point a, some of the light is reflected as ray Ra and and some is refracted following the path ab to the back of the film.
*At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray Rc. Ra and Rc are parallel. However, Rc has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if Ra and Rc are in phase they will undergo constructive interference and the region ac will be bright if Ra and Rc are out of phase, they will undergo destructive interference.
* Refraction at an interface never changes the phase of the wave.
* For reflection at the interface between two media 1 and 2, if n1<n2 the reflected wave will change phase by π.
if n1>n2 the reflected wave will not undergo a phase change. for reference nair=1.00
* if the waves are in phase after refection at all interfaces, then the effects of path length in the film are
Constructive interference occur when (n= refractive index) 2t=mλ/n m=0,1,2,3.....
Destructive interference occurs when 2t=(m+1/2)λ/n m=0,1,2,3...
Q. A 600 nm light is perpendicularly incident on a soap film suspended in air. The film is 1.00 μm thick with n=1.35. Which statement most accurately describes the interference of the light reflected by the two surfaces of the film?
View SolutionAssertion (A) : The soap film in sun light is colourful
Reason (R ) : Thin films produce interference of light
View SolutionThis question has a paragraph followed by two statements, Statement - 1 and Statement - 2. Of the given four alternatives after the statements, choose the one that describes the statements. A thin air film is formed by putting the convex surface of a plane-convex lens over a plane glass plate. With monochromatic light, this film gives an interference pattern due to light reflected from the top (convex) surface and the bottom (glass plate) surface of the film.
Statement - 1: When light reflects from the air-glass plate interface, the reflected wave suffers a phase change of π.
Statement - 2 : The centre of the interference pattern is dark.
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

6. If the thickness of film in above question in not technologically possible to manufacture, then next thickness of film required is (approximately)
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
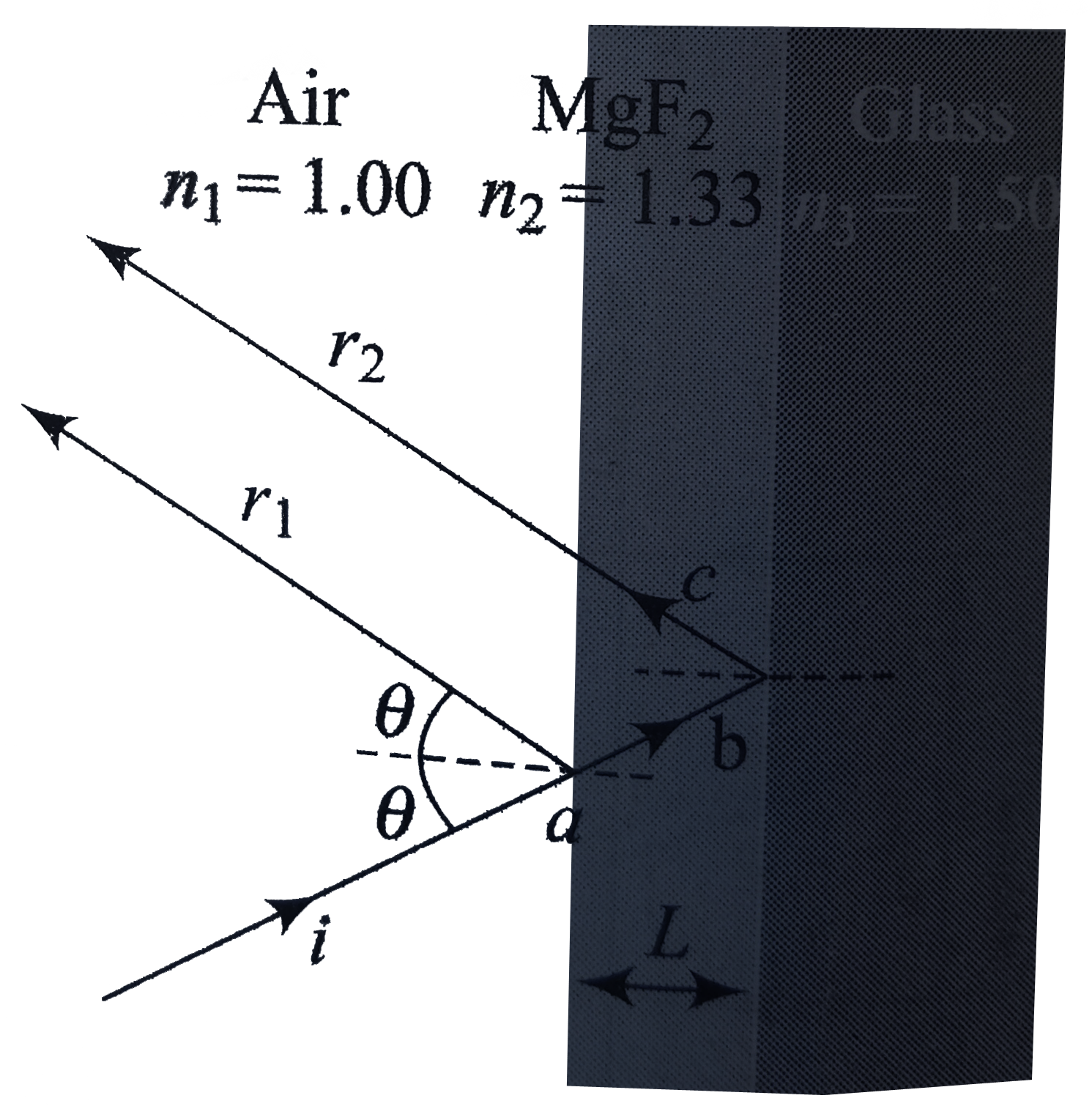
View Solution
