Student perform an experiment for measuring the acceleration due to gravity usinf a simple pendulum. They use lengths of the pendulum and // or record time for different number of oscillations . The observations are shown in the following table . Least count for length
Least count for time .
If , and are the percentage errors in , i.,e., for students I,II , and III, respectively , then
The correct Answer is:B
The greatest the volume of , the lesser the error . Hence , fractional error in the first observation in minimum.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple correct Answer Type
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Fill In The Blanks
4 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
The IUPAC name of CH3−CH∣CH3−C∣∣O−C∣∣O−NH∣Br is:
View SolutionStudents I1,J1,J3 and I2 perform an experiment for measuring the acceleration due to gravity (g) using a simple predulum, they use different lengths of the pendulum and record time for different number of oscillations. The observations are shown in the table. Least count for length =0.1cm, least count for time = 1s
StudentsLength of thependulum (cm)No.ofoscillations(n)Time periodof pendulum (s)I1100.02020J1400.01040J1100.01020I1400.02040
If P1,P2,P3 and P4 are the % error in g for students I1,J1,J3 and I2 respectively then -
View Solution
Knowledge Check
The name of C∣CHOH=C∣NH2H is
A1-Aminoprop-2-enalB3-Aminoprop-2-enalC1-Amino-2-formyletheneD3-Amino-1-oxoprop-2-eneIUPAC name of CH2∣CN−CH∣CN−CH2∣CN
A3 - cyanopentane -1, 5-dinitrileBPropane -1,2,3 - tri nitrileC1,2,3 - tri cyano propaneDPropane - 1,2,3 - tricarbonitri leIUPAC name of CH3−C∣∣O−CH∣C=O∣CH3−C∣∣O−OCH3
AMethyl-2, 2-acetyl ethanoateB2,2-acetyl-1-methoxy ethanoneCMethyl-2-acetyl-3-oxobutanoateDnone of these
Order of enolic content
(P)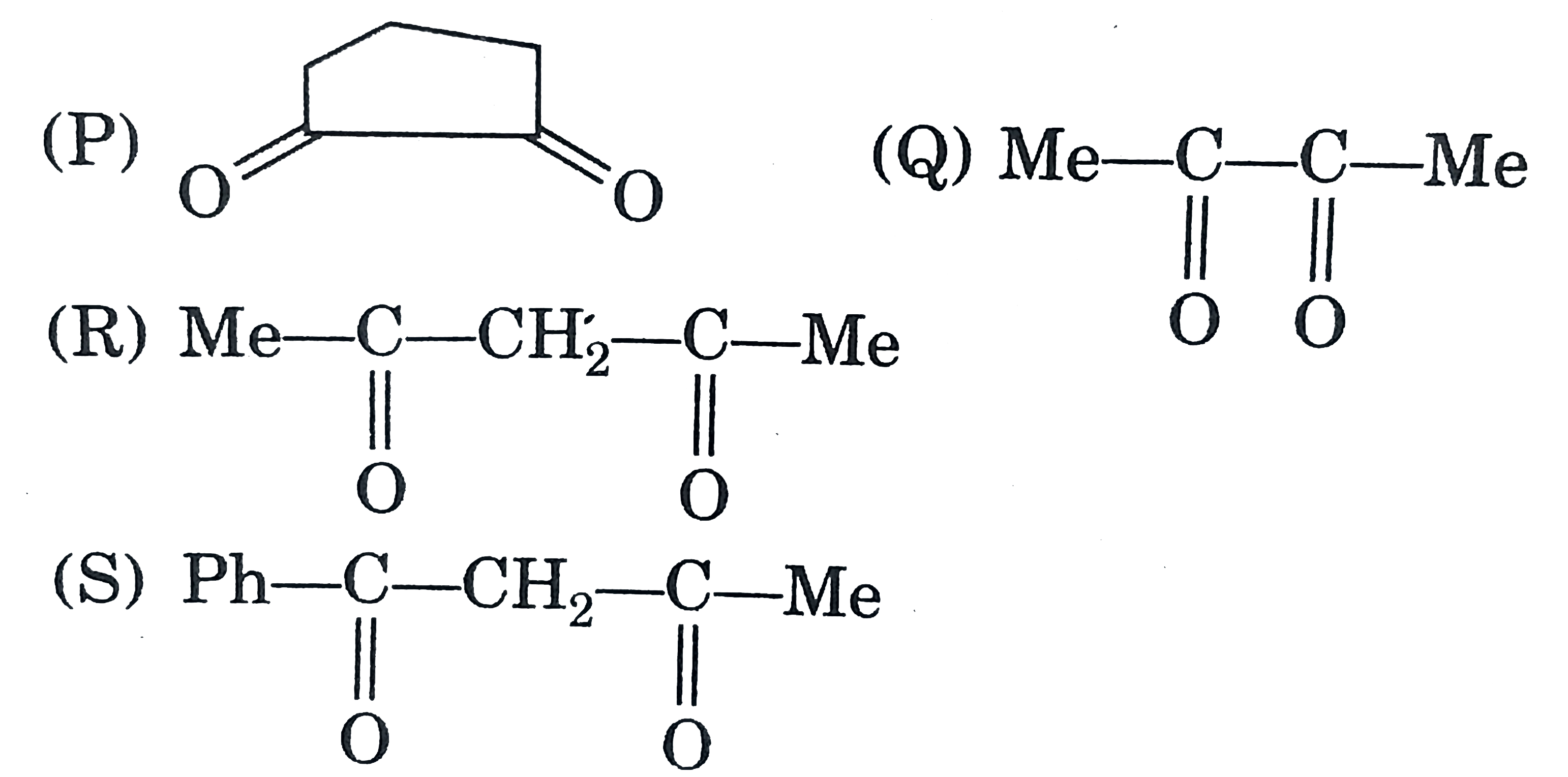
(Q) Me−C∣∣O−C∣∣O−Me
(S) Me−C∣∣O−CH2−C∣∣O−Me
View SolutionWhich of the following names are not correct for the given compound :
CH2∣CHO−CH∣CHO−CH2∣CHO
View SolutionThe IUPAC name of the compound
C∣OHH2−C∣OHH−C∣OHH2
View SolutionThe IUPAC name of CH2∣CN−CH∣CN−CH2∣CN is:
View SolutionWhich of the following names are not correct for the given compound?
CH2∣CHO−CH∣CHO−CH2∣CHO
View Solution
