Subtraction of vectors obeys
commutative law
Associative law
Distributive law
All the above
The correct Answer is:C
To solve the question "Subtraction of vectors obeys which law?", we can analyze the properties of vector subtraction in relation to the laws of addition and multiplication. Here’s a step-by-step breakdown:
Step 1: Understand the Laws of Vectors
Vectors can be added or subtracted, and there are certain mathematical laws that govern these operations. The main laws to consider are:
- Commutative Law
- Associative Law
- Distributive Law
Step 2: Analyze Commutative Law
The commutative law states that the order of addition does not matter:
A+B=B+A
For subtraction, however:
A−B≠B−A
This means that vector subtraction does not obey the commutative law.
Step 3: Analyze Associative Law
The associative law states that the way in which vectors are grouped does not affect their sum:
(A+B)+C=A+(B+C)
For subtraction, we have:
(A−B)−C≠A−(B−C)
This shows that vector subtraction does not obey the associative law either.
Step 4: Analyze Distributive Law
The distributive law states that multiplication distributes over addition:
C⋅(A+B)=C⋅A+C⋅B
For subtraction, we can express it as:
C⋅(A−B)=C⋅A−C⋅B
This shows that vector subtraction does obey the distributive law.
Conclusion
After analyzing all three laws, we conclude that vector subtraction does not obey the commutative or associative laws, but it does obey the distributive law. Therefore, the correct answer is:
Vector subtraction obeys the distributive law.
---
Vectors can be added or subtracted, and there are certain mathematical laws that govern these operations. The main laws to consider are:
- Commutative Law
- Associative Law
- Distributive Law
The commutative law states that the order of addition does not matter:
A+B=B+A
A−B≠B−A
This means that vector subtraction does not obey the commutative law.
The associative law states that the way in which vectors are grouped does not affect their sum:
(A+B)+C=A+(B+C)
(A−B)−C≠A−(B−C)
This shows that vector subtraction does not obey the associative law either.
The distributive law states that multiplication distributes over addition:
C⋅(A+B)=C⋅A+C⋅B
C⋅(A−B)=C⋅A−C⋅B
This shows that vector subtraction does obey the distributive law.
After analyzing all three laws, we conclude that vector subtraction does not obey the commutative or associative laws, but it does obey the distributive law. Therefore, the correct answer is:
Similar Questions
Assertion: The difference of two vectors A and B can be treated as the sum of two vectors.
Subtraction of vectors can be defined in terms of addition of vectors.
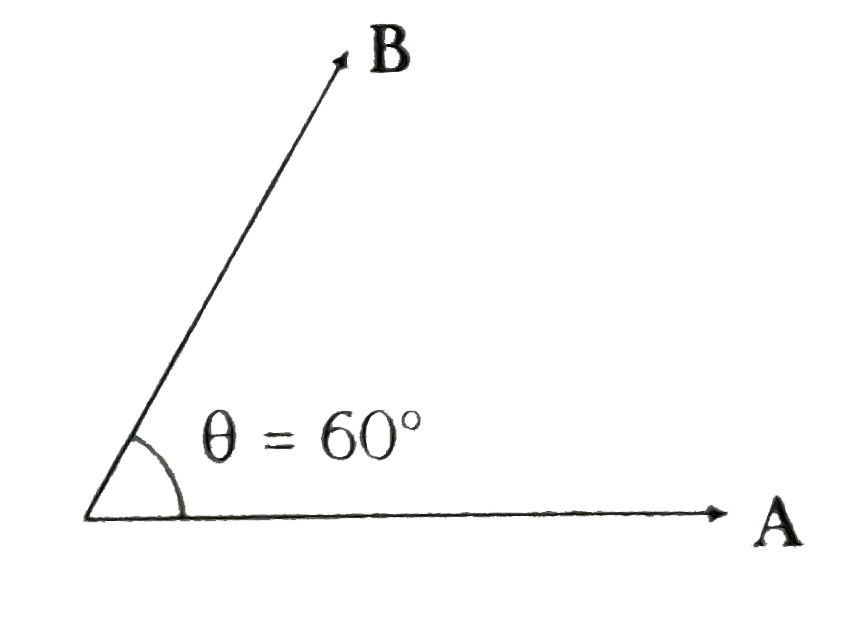
View SolutionFind the subraction of vector A and B as shown in the figure , also find the direction of subtraction vector ,Given A=4 unit and b=3 unit .
View SolutionAssertion: Two vectors are said to be equal if , and only if, they have the same magnitude and the same dirction.
Reason: Addition and subtraction of scalars make sense only for quantities with same units.
View SolutionAddition & Subtraction of Binary Numbers
View SolutionAssertion - Vector addition of two vector is always greater then their vector subtraction.
Reason At θ=90∘ , addition and subtraction of two vector are equal .
View SolutionState True or False:
Subtraction distributes over division.
View SolutionIf magnitude of sum of two unit vectors is √2 then find the magnitude of subtraction of these unit vectors.
View SolutionA : One of the images in double refraction doesn't obey the principles of refraction.
R : Extraordinary image in double refraction doesn't obey the principles of refraction because its velocity changes with direction.
View SolutionIf →Aand→B are non-zero vectors which obey the relation ∣∣→A+→B∣∣=∣∣→A−→B∣∣, then the angle between them is
View SolutionArrange the vectors subtractions so that their magnitudes are in decreasing order. If the two vectors →A and →B are acting at an angle (∣∣→A∣∣>∣∣→B∣∣)
a) 60° b) 90° c) 180° d) 120°
View Solution
