The vector subtraction………………………………bya vector.
To solve the problem of vector subtraction, let's break it down step by step.
Step 1: Understand Vector Subtraction
Vector subtraction involves taking one vector away from another. In mathematical terms, if we want to subtract vector b from vector a, we express this as:
→R=→a−→b
Step 2: Rewrite Vector Subtraction as Addition
To perform vector subtraction, we can rewrite it in terms of vector addition. Specifically, we can express the subtraction of vector b from vector a as:
→R=→a+(−→b)
Here, -b represents the vector b with its direction reversed.
Step 3: Draw the Vectors
Visualize the vectors:
- Draw vector a in its original direction.
- Draw vector b in its original direction.
- Then, draw -b (the negative of vector b) in the opposite direction of b but with the same magnitude.
Step 4: Add the Vectors
Now, we need to add vector a and vector -b. You can use the head-to-tail method or the parallelogram law of vector addition to find the resultant vector R.
1. Place the tail of vector -b at the head of vector a.
2. The resultant vector R will be drawn from the tail of vector a to the head of vector -b.
Step 5: Resultant Vector
The resultant vector R represents the result of the vector subtraction:
→R=→a−→b
Final Result
Thus, the vector subtraction of b from a gives us the resultant vector R.
---
Vector subtraction involves taking one vector away from another. In mathematical terms, if we want to subtract vector b from vector a, we express this as:
→R=→a−→b
To perform vector subtraction, we can rewrite it in terms of vector addition. Specifically, we can express the subtraction of vector b from vector a as:
→R=→a+(−→b)
Here, -b represents the vector b with its direction reversed.
Visualize the vectors:
- Draw vector a in its original direction.
- Draw vector b in its original direction.
- Then, draw -b (the negative of vector b) in the opposite direction of b but with the same magnitude.
Now, we need to add vector a and vector -b. You can use the head-to-tail method or the parallelogram law of vector addition to find the resultant vector R.
2. The resultant vector R will be drawn from the tail of vector a to the head of vector -b.
The resultant vector R represents the result of the vector subtraction:
→R=→a−→b
Thus, the vector subtraction of b from a gives us the resultant vector R.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Fill in the blanks11videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT multiple11videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Fill in the blanks10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the subraction of vector A and B as shown in the figure , also find the direction of subtraction vector ,Given A=4 unit and b=3 unit .
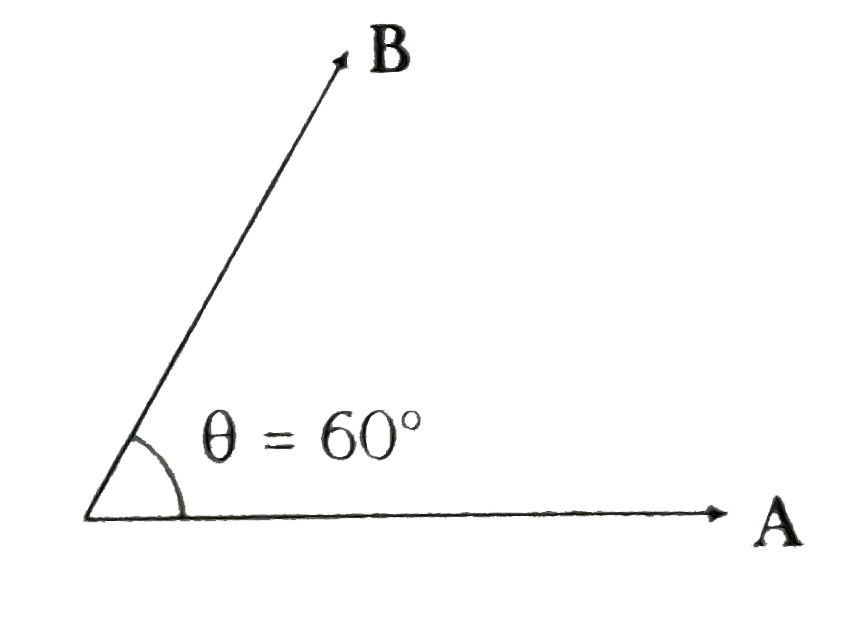 A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘
A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘ - Question 2 - Select One
Assertion: The difference of two vectors A and B can be treated as the sum of two vectors.
Subtraction of vectors can be defined in terms of addition of vectors.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both aseertion and reason are false. - Question 3 - Select One
Assertion - Vector addition of two vector is always greater then their vector subtraction.
Reason At θ=90∘ , addition and subreaction of two vector are equal .AIf both Assetion and Reason are correct but Reason is the correct explanation of Assertion.BIf both Assetion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Asserion is true but Reason is falseDIf Asserion is false but Reason is true
Arrange the vector subtractions so that their magnitude are in decreasing order. If the two vectors →A and →B are acting at an angle (∣∣→A∣∣>∣∣→B∣∣). (a) 60∘ (b) 90∘ (c) 180∘ (d) 120∘
View SolutionVectors subtraction is ___________
View SolutionIf the component of one vector in the direction of another vector is zero, then those two vectors are _______
View SolutionThe vector product of two vector is a vector whose direction is given is given by
View SolutionIf component of one vector in the direction of another vector is zero, then those two vectors
View Solution

