Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
To solve the problem of finding the charge on a capacitor when a charge +Q1 is given to the positive plate and a charge −Q2 is given to the negative plate, we can follow these steps:
Step 1: Understand the Charges on the Plates
A capacitor consists of two plates: one positively charged and one negatively charged. In this case, the positive plate has a charge of +Q1 and the negative plate has a charge of −Q2.
Step 2: Identify the Inner and Outer Surfaces
Each plate has two surfaces: an inner surface (facing the other plate) and an outer surface (facing away from the other plate). We denote:
- Surface 1: Outer surface of the positive plate
- Surface 2: Inner surface of the positive plate
- Surface 3: Inner surface of the negative plate
- Surface 4: Outer surface of the negative plate
Step 3: Apply Charge Distribution Principles
For a capacitor, the charge on the outer surfaces of the plates is influenced by the charge on the inner surfaces. The total charge on the capacitor can be determined by the charges on these surfaces.
Step 4: Calculate Charge on the Outer Surfaces
The charge on the outer surface of the positive plate (Surface 1) and the outer surface of the negative plate (Surface 4) can be expressed as:
Charge on Surface 1=Charge on Surface 4=Q1−Q22
Step 5: Calculate Charge on the Inner Surfaces
Now, we can find the charge on the inner surface of the positive plate (Surface 2) and the inner surface of the negative plate (Surface 3):
- Charge on Surface 2 (inner surface of the positive plate):
Charge on Surface 2=Q1−Charge on Surface 1=Q1−Q1−Q22=Q1+Q22
- Charge on Surface 3 (inner surface of the negative plate):
Charge on Surface 3=−(Charge on Surface 2)=−Q1+Q22
Step 6: Determine the Charge on the Capacitor
The charge on the capacitor is defined as the charge on the inner surface of the positive plate (Surface 2):
Charge on the capacitor=Q1+Q22
Final Answer
Thus, the charge on the capacitor is:
Charge on the capacitor=Q1+Q22
---
A capacitor consists of two plates: one positively charged and one negatively charged. In this case, the positive plate has a charge of +Q1 and the negative plate has a charge of −Q2.
Each plate has two surfaces: an inner surface (facing the other plate) and an outer surface (facing away from the other plate). We denote:
- Surface 1: Outer surface of the positive plate
- Surface 2: Inner surface of the positive plate
- Surface 3: Inner surface of the negative plate
- Surface 4: Outer surface of the negative plate
For a capacitor, the charge on the outer surfaces of the plates is influenced by the charge on the inner surfaces. The total charge on the capacitor can be determined by the charges on these surfaces.
The charge on the outer surface of the positive plate (Surface 1) and the outer surface of the negative plate (Surface 4) can be expressed as:
Charge on Surface 1=Charge on Surface 4=Q1−Q22
Now, we can find the charge on the inner surface of the positive plate (Surface 2) and the inner surface of the negative plate (Surface 3):
- Charge on Surface 2 (inner surface of the positive plate):
Charge on Surface 2=Q1−Charge on Surface 1=Q1−Q1−Q22=Q1+Q22
- Charge on Surface 3 (inner surface of the negative plate):
Charge on Surface 3=−(Charge on Surface 2)=−Q1+Q22
The charge on the capacitor is defined as the charge on the inner surface of the positive plate (Surface 2):
Charge on the capacitor=Q1+Q22
Thus, the charge on the capacitor is:
Charge on the capacitor=Q1+Q22
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A capacitor A of capacitance 4μF is charged to 30V and another capacitor B of capacitance 2μF is charged to 15V. Now, the positive plate of A is connected to the negative plate of B and negative plate of A to the positive plate of B. find the final charge of each capacitor and loss of electrostatic energy in the process.
View SolutionConsider a parallel plate capacitor having charge Q. Then,
View SolutionAn air capacitor consists of two parallel plates B as shown in the figure. Plate A is given a change and plate B is given a charge 3Q. P is the median plane of the capacitor. If C0 is the capacitor capacitor, then

View SolutionTwo parallel plates capacitors A and B having capacitance of 1μFand5μF are charged separately to the same potential of 100 V. Now, the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B. Find the final charges on each capacitors.
View SolutionA capacitor of 5μF is charged to a potential of 100V. Now, this charged capacitor is connected to a battery of 100V with the posiitive terminal of the battery connected to to the negative plate of the capacitor . For the given situation, mark the correct statement(s).
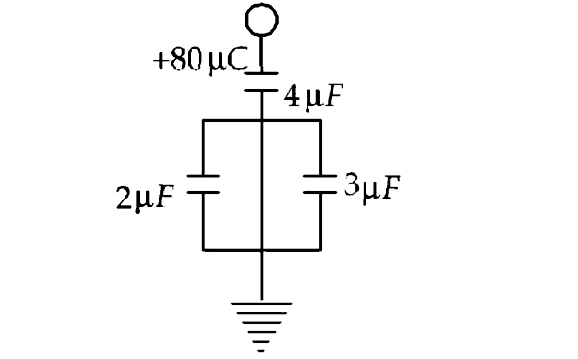
View SolutionIn the given circuit, a charge of +80μC is given to the upper plate of the 4μF capacitor. Then in the steady state, the charge on the upper plate of the 3μF capacitor is
View SolutionA parallel plate capacitor is charged. If the plates are pulled apart
View SolutionA capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
View SolutionIf the two plates of the charged capacitor are connected by a wire, then
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View Solution
