A dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
To solve the problem of how the force between the plates of an isolated capacitor changes when a dielectric slab is inserted, we can follow these steps:
1. Understand the System:
- We have an isolated parallel plate capacitor with charge Q on one plate and −Q on the other. The electric field E between the plates is determined by the charge and the area of the plates.
2. Electric Field Calculation:
- The electric field E between the plates of a parallel plate capacitor without a dielectric is given by:
E=σϵ0
- Where σ is the surface charge density, which can be expressed as:
σ=QA
- Thus, the electric field can be rewritten as:
E=Qϵ0A
3. Force Between the Plates:
- The force F between the plates of the capacitor can be calculated using the formula:
F=QE
- Substituting the expression for E:
F=Q(Qϵ0A)=Q2ϵ0A
4. Effect of Inserting a Dielectric:
- When a dielectric slab is inserted, the capacitance of the capacitor increases, but since the capacitor is isolated, the charge Q on the plates remains constant.
- The electric field E in the presence of a dielectric is given by:
E=Qϵ0Aκ
- Where κ is the dielectric constant of the material. However, since Q and A remain constant, the force can be expressed as:
F=Q(Qϵ0Aκ)=Q2ϵ0Aκ
5. Conclusion:
- Since the dielectric constant κ is greater than 1, the force F decreases when the dielectric is inserted. However, since the charge and area remain constant, the overall structure of the force equation indicates that the force remains unchanged in terms of its dependence on Q and A.
- Therefore, the force between the plates remains unchanged when a dielectric slab is inserted into an isolated capacitor.
Final Answer:
The force between the plates will remain unchanged.
---
- We have an isolated parallel plate capacitor with charge Q on one plate and −Q on the other. The electric field E between the plates is determined by the charge and the area of the plates.
- The electric field E between the plates of a parallel plate capacitor without a dielectric is given by:
E=σϵ0
- Where σ is the surface charge density, which can be expressed as:
σ=QA
- Thus, the electric field can be rewritten as:
E=Qϵ0A
- The force F between the plates of the capacitor can be calculated using the formula:
F=QE
- Substituting the expression for E:
F=Q(Qϵ0A)=Q2ϵ0A
- When a dielectric slab is inserted, the capacitance of the capacitor increases, but since the capacitor is isolated, the charge Q on the plates remains constant.
- The electric field E in the presence of a dielectric is given by:
E=Qϵ0Aκ
- Where κ is the dielectric constant of the material. However, since Q and A remain constant, the force can be expressed as:
F=Q(Qϵ0Aκ)=Q2ϵ0Aκ
- Since the dielectric constant κ is greater than 1, the force F decreases when the dielectric is inserted. However, since the charge and area remain constant, the overall structure of the force equation indicates that the force remains unchanged in terms of its dependence on Q and A.
- Therefore, the force between the plates remains unchanged when a dielectric slab is inserted into an isolated capacitor.
The force between the plates will remain unchanged.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
When a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionA dielectric slab is inserted between the plates of an isolatted charged capacitor. Which of the following quantities will remain the same?
View SolutionAssertion: A dielectric slabis inserted between plates of an isolated capacitor. charge on capacitor will remain same.
Reason Charge on an isolated system is conserved.
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
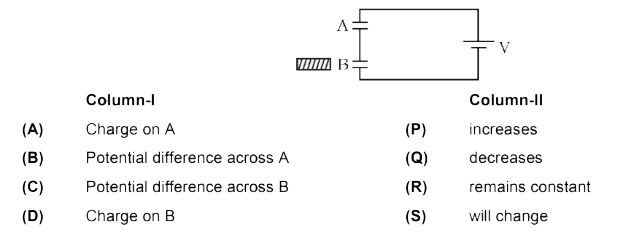
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionThe capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionThe capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution
