Suppose a disc is rotating counter clockwise in the plane of the paper then
It's angular velocity vector will be perpendicular to the page pointing up out of the page
It's angular velocity vector will be perpendicular to the page pointing inwards
It's angular velocity vector acts along the tangent to the disc.
none of the above is correct
The correct Answer is:A
To solve the question regarding the rotation of a disc in the plane of the paper, we need to analyze the situation step by step.
1. Understanding the Rotation Direction:
- The disc is rotating counterclockwise. This means that if you were to look down at the disc from above, it would be spinning in the opposite direction to the movement of the hands of a clock.
2. Identifying the Angular Velocity Vector:
- The angular velocity vector (→ω) is a vector that describes the axis of rotation and the speed of rotation. By the right-hand rule, if you curl the fingers of your right hand in the direction of the rotation (counterclockwise), your thumb will point in the direction of the angular velocity vector.
3. Applying the Right-Hand Rule:
- For a counterclockwise rotation, when you apply the right-hand rule, your thumb points upwards, out of the plane of the paper. This indicates that the angular velocity vector is directed out of the page.
4. Evaluating the Given Options:
- Option 1: "Its angular velocity will be perpendicular to the page pointing up out of the page." This is correct based on our analysis.
- Option 2: "Its angular velocity will be perpendicular to the page pointing inwards." This is incorrect because the angular velocity points outwards.
- Option 3: "Its angular velocity vector acts along the tangent to the disk." This is incorrect as the angular velocity vector is not tangent but rather perpendicular to the plane of rotation.
- Option 4: "None of the above." This is incorrect since we have identified a correct option.
5. Conclusion:
- The correct statement is Option 1: "Its angular velocity will be perpendicular to the page pointing up out of the page."
Final Answer:
The correct option is Option 1.
---
- The disc is rotating counterclockwise. This means that if you were to look down at the disc from above, it would be spinning in the opposite direction to the movement of the hands of a clock.
- The angular velocity vector (→ω) is a vector that describes the axis of rotation and the speed of rotation. By the right-hand rule, if you curl the fingers of your right hand in the direction of the rotation (counterclockwise), your thumb will point in the direction of the angular velocity vector.
- For a counterclockwise rotation, when you apply the right-hand rule, your thumb points upwards, out of the plane of the paper. This indicates that the angular velocity vector is directed out of the page.
- Option 1: "Its angular velocity will be perpendicular to the page pointing up out of the page." This is correct based on our analysis.
- Option 2: "Its angular velocity will be perpendicular to the page pointing inwards." This is incorrect because the angular velocity points outwards.
- Option 3: "Its angular velocity vector acts along the tangent to the disk." This is incorrect as the angular velocity vector is not tangent but rather perpendicular to the plane of rotation.
- Option 4: "None of the above." This is incorrect since we have identified a correct option.
- The correct statement is Option 1: "Its angular velocity will be perpendicular to the page pointing up out of the page."
The correct option is Option 1.
Similar Questions
If a disc starting from rest acquires an angular velocity of 240rev min−1 in 10 s, then its angular acceleration will be
View SolutionIn example number 12.16 suppose the disc starts rotating anticlockwise with the same angular velocity ω=vR, then what will be the angular momentum of the disc about bottommost in this new situation?
View Solution
Knowledge Check
There is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
Acurrent is induced in the loop in the anti-clockwise directionBcurrnet is induced in the loop in the clockwise direction.Cac is induced in the loop.Dno current is induced in the loop.
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
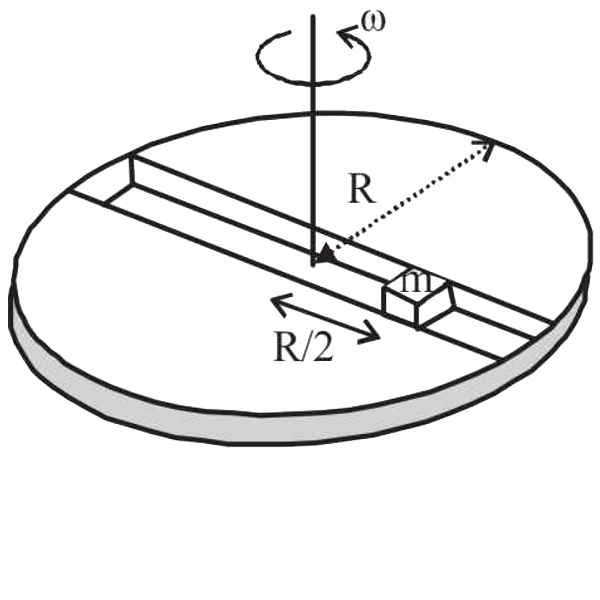
The net reaction of the disc on the block is
View SolutionThere is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
View SolutionTwo discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View SolutionA positively charged disk is rotated clockwise as shown in Fig. The direction of hte magnetic field at a point A in the plane of the disk is
View SolutionAn ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
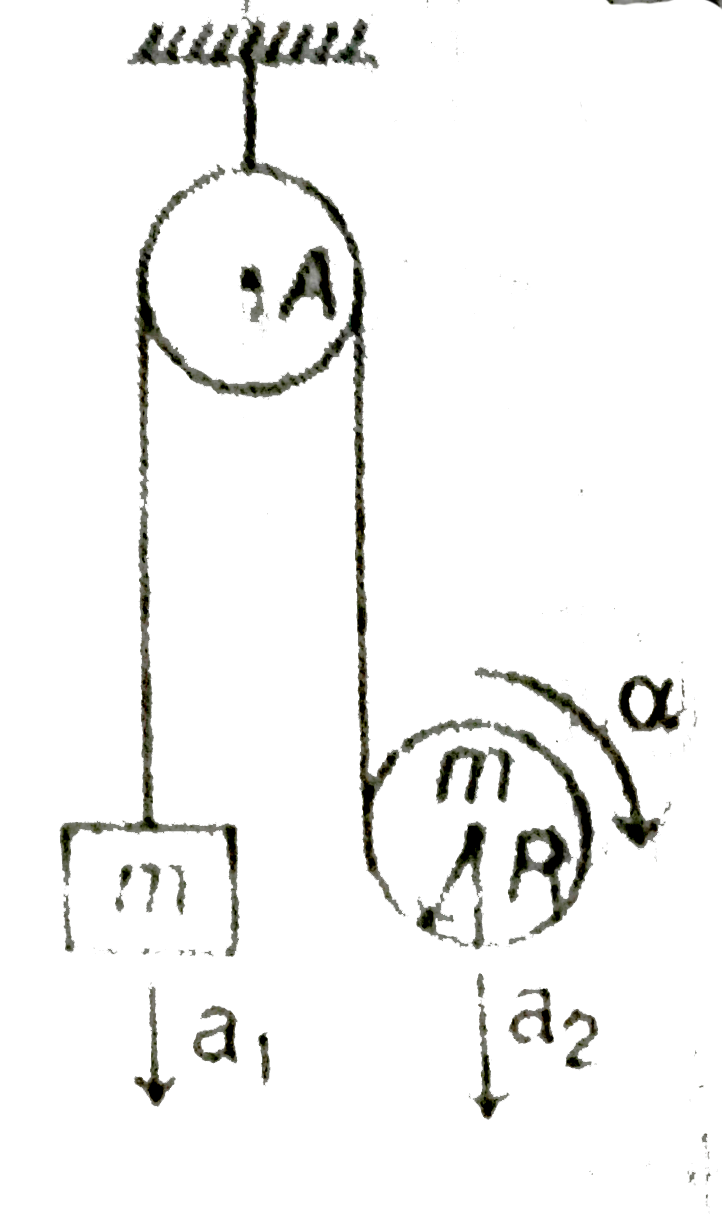
View SolutionThe magnetic field B shown in is directed into the plane of the paper. ACDA is a semicircular conducting loop of radius r with the centre at O. The loop is now made ot rotate clockwise with a constant angular velocity ω about on axis passing through O and perpendicular to the plane of the paper. The resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop. Plot a graph between the induced current i and ωt, for two periods of rotation.

View SolutionThe figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separted. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,
View Solution
