There is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then
current is induced in the loop in the anti-clockwise direction
current is induced in the loop in the clockwise direction
AC is induced in the loop
No current is induced in the loop
The correct Answer is:A
To solve the problem, we need to analyze the situation step by step:
Step 1: Understand the Magnetic Field
The problem states that there is a uniform magnetic field directed perpendicular and into the plane of the paper. This means that the magnetic field lines are pointing towards the observer (represented by crosses in diagrams).
Hint: Visualize the magnetic field direction; it helps in understanding how it interacts with the loop.
Step 2: Analyze the Conducting Loop
We have an irregularly shaped conducting loop that is changing into a circular loop. As the shape of the loop changes, the area of the loop is also changing.
Hint: Remember that the area of the loop is crucial because it affects the magnetic flux through the loop.
Step 3: Determine the Change in Area
As the irregular loop transforms into a circular loop, the area of the loop increases. This increase in area leads to a change in magnetic flux through the loop.
Hint: Recall the formula for magnetic flux: Φ=B×A, where B is the magnetic field strength and A is the area of the loop.
Step 4: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's Law, a change in magnetic flux through a loop induces an electromotive force (emf) in the loop. The induced emf will generate a current in the loop.
Hint: Faraday's Law states that the induced emf is proportional to the rate of change of magnetic flux.
Step 5: Determine the Direction of Induced Current
Lenz's Law states that the direction of the induced current will be such that it opposes the change in magnetic flux. Since the area of the loop is increasing, the magnetic flux through the loop is also increasing.
- The magnetic field is directed into the paper, and since the flux is increasing in this direction, the induced current must create a magnetic field that opposes this increase.
- To oppose the increase in flux (which is into the paper), the induced current must flow in an anticlockwise direction (as viewed from above).
Hint: Use the right-hand rule to determine the direction of the induced current based on the direction of the magnetic field and the change in flux.
Step 6: Conclusion
The induced current in the loop is in the anticlockwise direction.
Final Answer: The current induced in the loop is in the anticlockwise direction.
The problem states that there is a uniform magnetic field directed perpendicular and into the plane of the paper. This means that the magnetic field lines are pointing towards the observer (represented by crosses in diagrams).
We have an irregularly shaped conducting loop that is changing into a circular loop. As the shape of the loop changes, the area of the loop is also changing.
As the irregular loop transforms into a circular loop, the area of the loop increases. This increase in area leads to a change in magnetic flux through the loop.
According to Faraday's Law, a change in magnetic flux through a loop induces an electromotive force (emf) in the loop. The induced emf will generate a current in the loop.
Lenz's Law states that the direction of the induced current will be such that it opposes the change in magnetic flux. Since the area of the loop is increasing, the magnetic flux through the loop is also increasing.
- To oppose the increase in flux (which is into the paper), the induced current must flow in an anticlockwise direction (as viewed from above).
The induced current in the loop is in the anticlockwise direction.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrance special format questions
Explore 17 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example
Explore 71 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Space is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
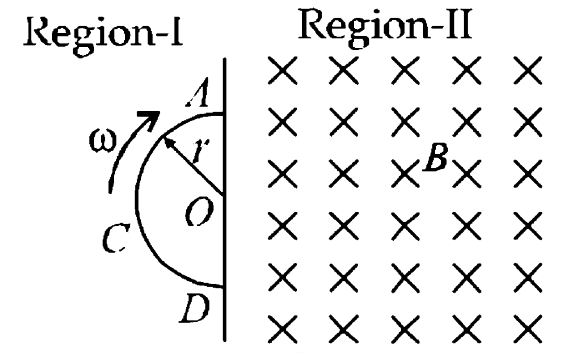
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.

(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionThe counductor AD moves to the right in a uniform magnetic field directed into the plane of the paper.

View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will be
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

External force required to maintain constant velocity of the loop for x=−95a will be
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=−9a/5, magnitude of induced current and its direction as seen from above will be:
View SolutionThere is a magnetic field acting in a plane perpendicular to this sheet of paper, downward into the paper as shown in the figure. Paticles in acuum move in the plane of the paper from left to right. The path indicated by the arrow could be travelled by

View Solutionthe uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionThe magnetic field B shown in is directed into the plane of the paper. ACDA is a semicircular conducting loop of radius r with the centre at O. The loop is now made ot rotate clockwise with a constant angular velocity ω about on axis passing through O and perpendicular to the plane of the paper. The resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop. Plot a graph between the induced current i and ωt, for two periods of rotation.

View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View Solution