Suppose a gas is heated up to a temperature at which all degrees of freedom (translational, rotational, and vibrational) of its molecules are excited. Find the molar heat capacity of such a gas in the isochoric process, as well as the adiabatic exponent γ, if the gas consists of
(a) diatomic ,
(b) linear N−atomic ,
( c) network N−atomic molecules.
(a) A diatomic molecule has 3 translational, 2 rotational and one vibrational degrees of freedom. The corresponding energy per mole is
3RT,(translational)+2×12RT,(for rotational)
+1×RT,(for vibrational)=72RT
Thus, CV=72R, and γ=CpCV=97
(b) For linear N−atomic molecules energy per mole
=(3N−52)RT as before
So, CV=(3N−52)R and γ=6N−36N−5
( c) For noncollinear N−atomic molecules
CV=3(N−1)R as before (2.68)γ=3N−23N−3=N−2/3N−1.
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy
47 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The First Law Of Thermodynamics - Heat Capacity
36 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Find the molar heat capacity of an ideal gas with adiabatic exponent γ for the polytorpic process PVn= Constant.
View SolutionA gas consisting of N−atomic molecules has the temperature T at which all degrees of freedom (translational, rotational, and vibrational) are excited. Find the mean energy of molecules in such a gas. What fraction of this energy corresponds to that of translational motion ?
View Solution
Knowledge Check
If the molar heat capacity of a gas in the process PT= constant is 5R, the number of degrees of freedom of molecules in the gas is
A4B5C6D3An ideal gas consists of molecules, each molecule being a linear chain of four atoms. If this gas is heated up to a temperature at which all degrees of freedom, including vibrational, are excited, the molar specific heat of such a gas at constant volume will be (include vibrational degrees also)
A19R2B15R2C6RD9RThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure. The molar heat capacity of gas during this process is [R is gas constant]
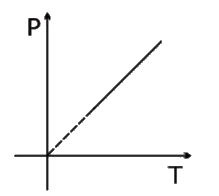 A1.7 RB3.25 RC2.5 RD4.2 R
A1.7 RB3.25 RC2.5 RD4.2 R
Find the adiabatic exponent γ for a mixture consisting of v1 moles of a monatomic gas and v2 moles of gas of rigid diatomic molecules.
View SolutionAn ideal gas consisting of N−atomic molecules is expanded isobarically. Assuming that all degrees of freedom (translational, rotational, and vibrational) of the molecules are excited, find what fraction of heat transferred to the gas in this process is spend to perform the work of expansion. Now high is this fraction in the case of monatomic gas ?
View SolutionFind the molar heat capacity of an ideak gas in a polytropic process pVn=const if the adiabatic exponent of the gas is equal to γ. At what values of the polytropic constant n will the heat capacity of the gas be negative ?
View SolutionA gas consisting of monatomic molecules (degrees of freedom = 3) was expanded in a polytropic process so that the rate of collisions of the molecules against the vessel's wall did not change. Find the molar heat capacity of the gas in the process.
View SolutionA diatomic ideal gas is heated at constant volume until its pressure becomes three times. It is again heated at constant pressure until its volume is doubled. Find the molar heat capacity for the whole process.
View Solution
