Find the molar heat capacity of an ideal gas with adiabatic exponent γ for the polytorpic process PVn= Constant.
To find the molar heat capacity C of an ideal gas undergoing a polytropic process described by the equation PVn=constant, we will follow these steps:
Step 1: Understand the First Law of Thermodynamics
The first law of thermodynamics states:
Q=ΔU+W
where Q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the gas.
Step 2: Express Heat Transfer and Work Done
For an ideal gas, the heat transfer can be expressed as:
Q=nCΔT
where C is the molar heat capacity and ΔT is the change in temperature.
The change in internal energy for an ideal gas is given by:
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume.
The work done in a polytropic process can be expressed as:
W=nR(T1−T2)n−1
where R is the universal gas constant, and T1 and T2 are the initial and final temperatures, respectively.
Step 3: Substitute into the First Law Equation
Substituting the expressions for Q, ΔU, and W into the first law gives us:
nCΔT=nCVΔT+nR(T1−T2)n−1
Step 4: Rearrange the Equation
Rearranging the equation to isolate C:
nCΔT−nCVΔT=nR(T1−T2)n−1
Factoring out nΔT from the left side:
n(C−CV)ΔT=nR(T1−T2)n−1
Step 5: Simplify the Equation
Dividing both sides by nΔT (assuming ΔT≠0):
C−CV=R(T1−T2)(n−1)ΔT
This can be simplified to:
C=CV+Rn−1
Step 6: Substitute the Value of CV
We know that for an ideal gas, the molar heat capacity at constant volume is:
CV=Rγ−1
Substituting this into our equation gives:
C=Rγ−1+Rn−1
Step 7: Final Expression for Molar Heat Capacity
Combining the terms:
C=R(1γ−1+1n−1)
Conclusion
Thus, the molar heat capacity C for the ideal gas undergoing a polytropic process is:
C=R(1γ−1+1n−1)
The first law of thermodynamics states:
Q=ΔU+W
where Q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the gas.
For an ideal gas, the heat transfer can be expressed as:
Q=nCΔT
where C is the molar heat capacity and ΔT is the change in temperature.
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume.
W=nR(T1−T2)n−1
where R is the universal gas constant, and T1 and T2 are the initial and final temperatures, respectively.
Substituting the expressions for Q, ΔU, and W into the first law gives us:
nCΔT=nCVΔT+nR(T1−T2)n−1
Rearranging the equation to isolate C:
nCΔT−nCVΔT=nR(T1−T2)n−1
Factoring out nΔT from the left side:
n(C−CV)ΔT=nR(T1−T2)n−1
Dividing both sides by nΔT (assuming ΔT≠0):
C−CV=R(T1−T2)(n−1)ΔT
This can be simplified to:
C=CV+Rn−1
We know that for an ideal gas, the molar heat capacity at constant volume is:
CV=Rγ−1
Substituting this into our equation gives:
C=Rγ−1+Rn−1
Combining the terms:
C=R(1γ−1+1n−1)
Thus, the molar heat capacity C for the ideal gas undergoing a polytropic process is:
C=R(1γ−1+1n−1)
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - SOLVED PROBLEMS SUBJECTIVE
18 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - SOLVED PROBLEMS OBJECTIVE
15 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
Similar Questions
Knowledge Check
The molar heat capacity for an ideal gas cannot
Abe negativeBbe equal to either CV or CPClie in the range CV≤C≤CPDit may have any value between −∞ and +∞The molar heat capacity of a gas in a process
Ais either CVorCPBlies between CVorCPCmay range from zero to infinityDcan have any real valueThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
 A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1)
A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1)
One mole of an ideal gas with the adiabatic exponent γ goes through a polytropic process as a result of which the absolute temperature of the gas increases τ−fold. The polytropic constant equal n. Find the entropy increment of the gas in this process.
View SolutionFind the molar heat capacity of an ideak gas in a polytropic process pVn=const if the adiabatic exponent of the gas is equal to γ. At what values of the polytropic constant n will the heat capacity of the gas be negative ?
View SolutionSuppose a gas is heated up to a temperature at which all degrees of freedom (translational, rotational, and vibrational) of its molecules are excited. Find the molar heat capacity of such a gas in the isochoric process, as well as the adiabatic exponent γ, if the gas consists of
(a) diatomic ,
(b) linear N−atomic ,
( c) network N−atomic molecules.
View SolutionFind the molar heat capacity (in terms of R) of a monoatomic ideal gas undergoing the process: PV1/2=constant?
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
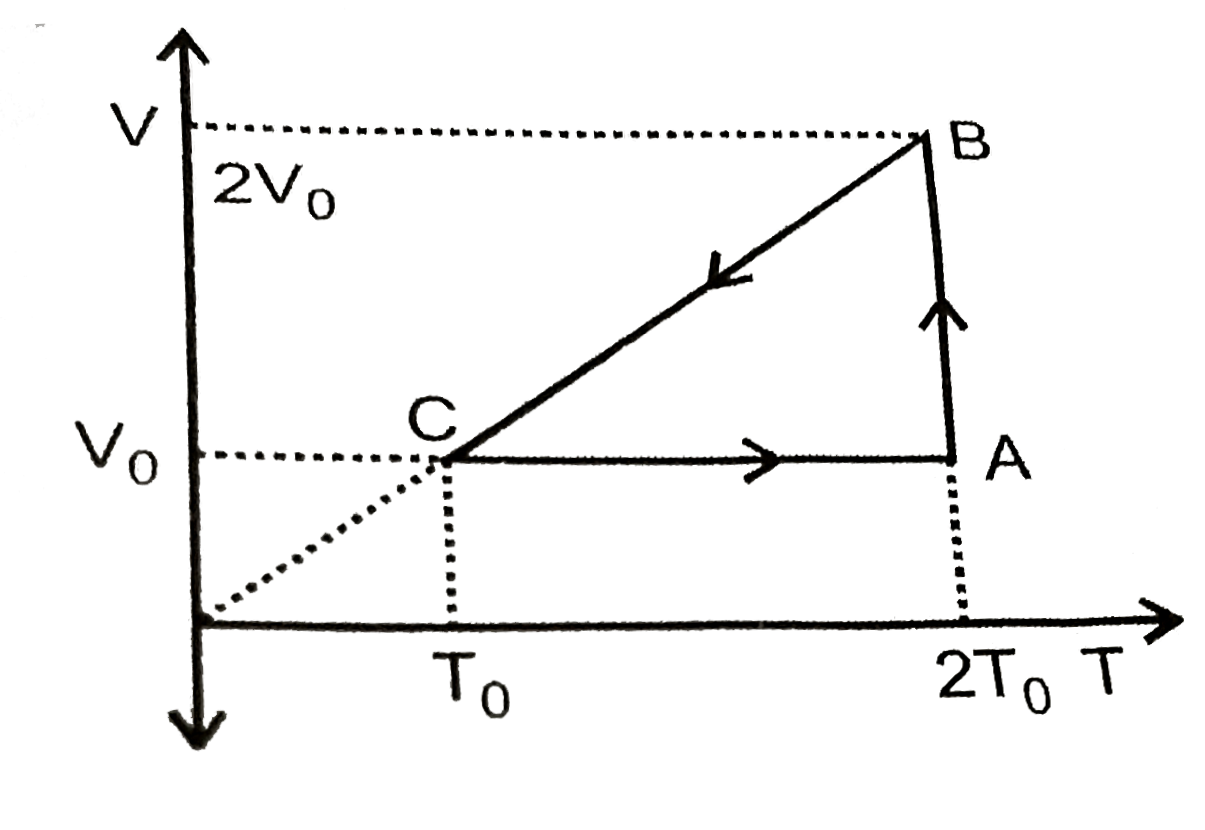
View Solution