Suppose that η0 is the ratio of the molecular concentration of hydrogen to that of nitrogen at the Earth's surface, while η is the corresponding ratio at the height h=3000m. Find the ratio η/η0 at the temperature T=280K, assuming that the temperature and the free fall acceleration are independent of the height.
η=condetration of H2concentration of N2=η0e−MH2gh/RTe−MN2−gh/RT=η0e(MN2−MH2)gh/RT
So more N2 at the bottom, (ηη0=1.39here).
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy
47 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The First Law Of Thermodynamics - Heat Capacity
36 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An ideal gas of molar mass M is contained in a tall vertical cylindrical vessel whose base area is S and height h. The temperatuer of the gas is T, its pressure on the bottom bass is p0. Assuming the temperature and the free-fall acceleration g to be independent of the height, find the mass of gas in the vessel.
View SolutionA tall vertical vessel contains a gas composed of two kinds of molecules of masses m1 and m2 . With m2>m1. The concentrations of these molecules at the bottom of the vessel are equal to n1 and n2 respectively, with n2>n1. Assuming the temperature T and the free-fall acceleration g to be independent of the height, find the height at which the concentrations of these kinds of molecules are equal.
View SolutionFind the force exerted on a particle by a uniform field if the concentrations of these particles at two levels separated by the distance Δh=30cm (along the field) differ by η=2.0 times. The temperature of the system is equal to T=280K.
View SolutionFind the mass of all molecules leaving one square centimetre of water surface per second into a saturated water vapour above it at a temperature t=100∘C. It is assumed that η=3.6% of all water vapour molecules falling on the water surface are retained in the liquid phase.
View SolutionLet us assume that air is under standard conditions close to the Earth's surface. Presuming that the temperature and the molar mass of air are independent of height, find the air pressure at the height 5.0km over the surface and in a mine at the depth 5.0km below the surface.
View Solution(a) Assume the atmosphere as an ideal gas in static equilibrium at constant temperature T0. The pressure on the ground surface is P0. The molar mass of the atmosphere is M. Calculate the atmospheric pressure at height h above the ground.
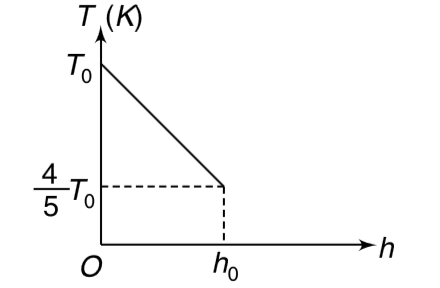
(b) To be more realistic, let as assume that the temperature in the troposphere (lower part of the atmosphere) decreases with height as shown in the figure. Now calculate the atmospheric pressure at a height h0 above the ground.
View SolutionAssuming the temperature and the molar mass of air, as well as the free-fall acceleration, to be independent of the height, find the difference in heights at which the air densities at the temperature 0∘C differ.
(a) e times ,
(b) by η=1.0%.
View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in fig if the ratio of the mass of wedge to that of the rod equals η and the friction between the contact surfaces are negligible.
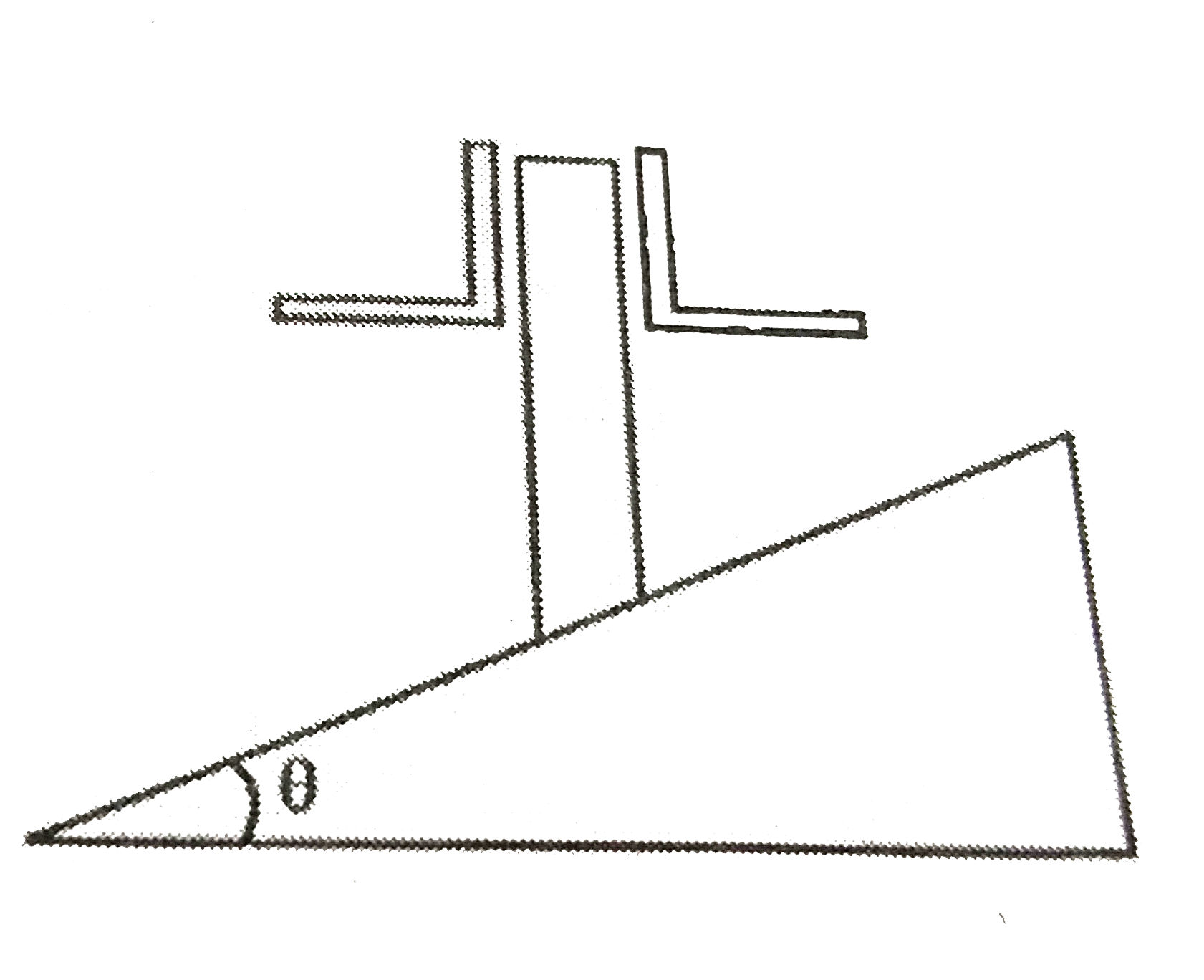
View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

View SolutionA horizontal tube of length l=100cm closed form both ends is displaced lengthwise with a constant acceleration ω. The tube contains argon at a temperature T=300K. At what value of ω will the argon concentrations at the tube's ends differ by η=1.0% ?
View Solution
