Taking into account that the wave phase ωt−kx is an invariant, i.e. it retains its value on transition from one interial frame to another, determine how the frequency ω and the wave number k entering the expression for the wave phase are transformed. Examine the unidimensional case.
From the invatiance of phase under Lorentz transformations we get
ω−kx=ω't'−k'x'
Here ω=ck. The primed corrdinates refer to the frame S' which is moving to the right with velocity v:-
Then x'=γ(x−vt)
t'=γ(t−vxc2)
where γ=(√1−v2/c2)−1
Substituting and equating the coefficients of t&x
ω=γω'+γk'v=ω'1+v/c√1−v2/c2
k=γω'vc2+γk'=k'1+v/c√1−v2/c2

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation
47 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
In a certain experiment , a sound wave was observed to have undergone a change in its velocity and wavelength but the frequency remained the same .
In another experiment , no change was observed in the velocity , wavelength or frequency but there was a change in the phase . if the direction of the wave propagation is changed in both the cases , identify the phenomena that took place in the two experiments . Give reasons for the changes in the physical quantities .
View SolutionA neutron with kinetic energy T=2m0c2, where m0 is its rest mass, strikes another, stationary, neutron. Determine:
(a) the combined kinetic energy ˜T of both neutrons in the frame of their centre of inertia and the momentum ˜p of each neutron in that frame,
(b) the velocity of the centre of inertia of this system of particles.
Instruction. Make use of the invariant E2−p2c2 remaining constant on transition from one inertial reference frame to another (E is the total energy of the system, p is its composite momentum).
View Solution
Knowledge Check
Huygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
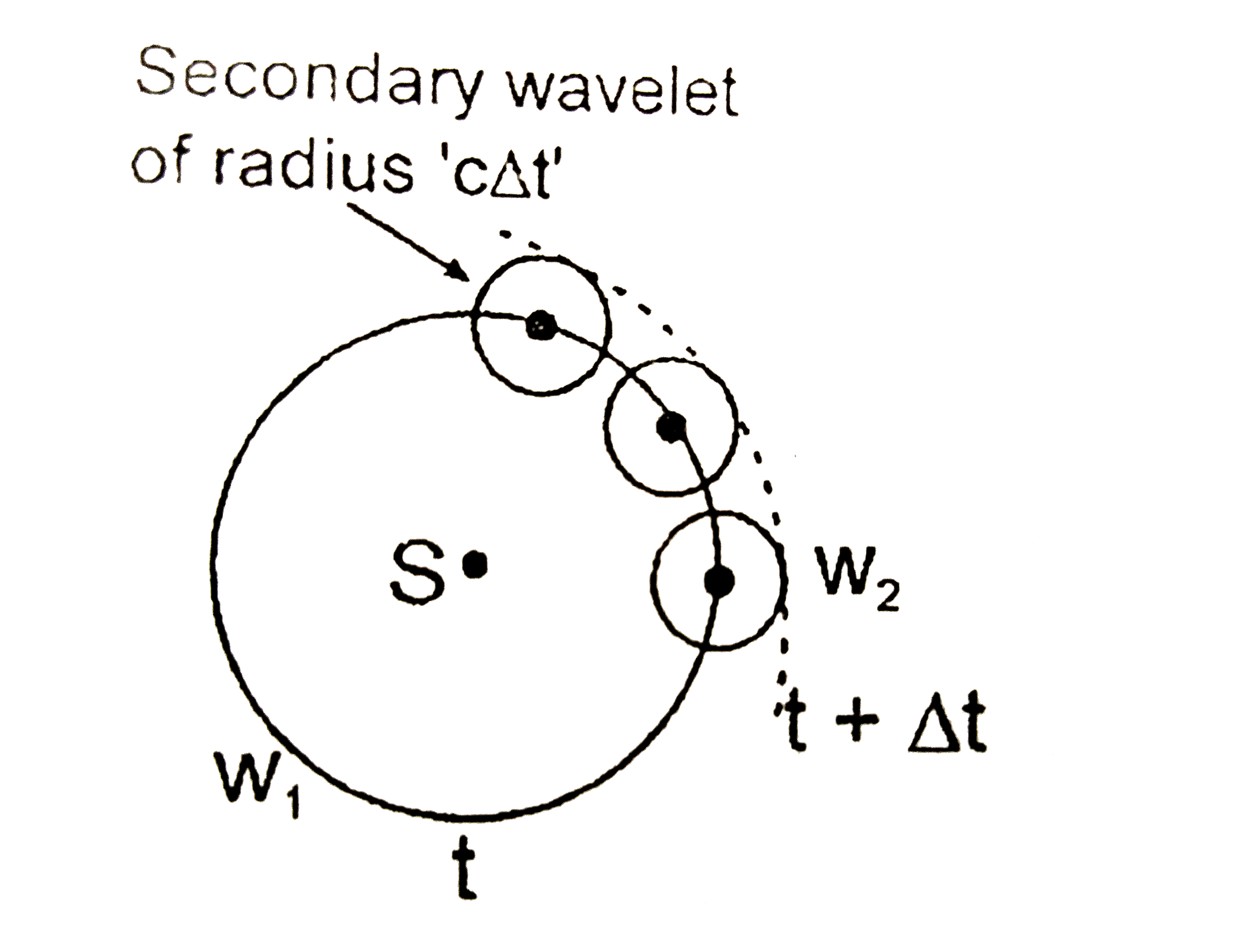
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)Ax+y+z=ctBx2+y2+z2=t2Cxy+yz+zx=c2t2Dx2+y2+z2=c2t2The electrons in a poly -electronic atom are filled one by one in roder fo increasing energy level . The enrgy fo subsgells and orientation depeds upon the values of three quantum numbers 9 i.e., n. l and m respectively derived from Schrodinger wave equation . The different orbitals fo a subsshells however possess same energy level and are called degenerater orbitals but their enrgy level charges in presenct of magentic field and the orbitals are non-degenerate . (A) spectral line is noticed it an electron jups form one level to tohere . the paramgnetic nature of eelment sis due to the presence of unpaired electron .
The number of spherical and angular nodes in 2p orbitals are :A1,1B2,1C1,0D0,1
One of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy.
The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state.
Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively.
When electrons return form n2 to n1 state, the number of lines in the spectrum will equal to
(n2−n1)(n2−n1+1)2
If the electon comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as :
E2−E1=ΔE,δE⇒hcλ
Since, h and c are constant, δE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula
¯v=R(1n21−1n22).
where R is a Rydberg's constant (R=1.1×107m−1)
The emission spectra is observed by the consequence of transition of electrons from higher energy state to ground state of He+ ion. Six different photons are observed during the emission spectra, then what will be the minimum wavelength during the transition?
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy.
The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state.
Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively.
When electrons return form n2 to n1 state, the number of lines in the spectrum will equal to
(n2−n1)(n2−n1+1)2
If the electon comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as :
E2−E1=ΔE,δE⇒hcλ
Since, h and c are constant, δE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula
¯v=R(1n21−1n22).
where R is a Rydberg's constant (R=1.1×107m−1)
What transition in the hydrogen spectrum would have the same wavelength as Balmer transitio, n=4 to n=2 in the He+ spectrum?
View SolutionA string of length L fixed at both ends vibrates in its fundamental mode at a frequency v and a maximum amplitude A. (a) Find the wavelength and the wave number k. (b) Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
View SolutionA long solenoid of length l=2.0 m , radius r=0.1 m and total number of turns N=1000 is carrying a current i0=20.0A. The axis of the solenoid conicides with the z-axis.
(a) State the expression for the magnetic field of the solenoid and calculate its value ? Magnetic field.
(b) Obtain the expression for the self - inductance (L) of the solenoid. Calcuate its value. Value of L .
( c) Calculate the energy stored (D) when the solenoid carries this current ?
(d) Let the resistance of the solenoid be R. It is connected to a battery of emf e. Obtain the expression for the current (i) in the solenoid.
(e) Let the solenoid with resistance R describe in part (d) be strecthed at a constant speed u ( l is increased but B and γ are constant ). State kirchhoff's second law for this cases. (Note: Do not solve for the current )
(f) Consider a time varying current i=i0cos(ωt) (where i0=20.0A) flowing in the solenoid. Obtain an expression for the electric field due to the current in the solenoid. (Note: Part(e) is not operative, i.e., the solenoid is not being stretched. )
(g) Consider t=π/2ωandω=200/πrad−s−1 in the previous part. Plot the magnitude of the electric field as a function of the radial distance from the solenoid. Also, sketch the electric lines of force.
View SolutionConsider a string fixed at one end . A travelling wave given by the wave equation y=Asin(ωt−kx) is incident on it . ltbr gt Show that at the fixed end of a string the waves suffers a phase change of π, i.e., as it travels back as if the wave is inverted.
View Solution(a) (i) Two independent mono chromatic sources of light cannot produced a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude ''a'' and frequency ''w'', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given byy3=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View Solution
