Tarzan (m=85.0kg) tries to cross a river by swinging on a vine . The vine is 10.0m just and his speed at the bottom of the swing (as he just clears the water) will be 8.00ms−1 Tarzan does not know that the vine hasa breaking strenght of 1000N Does he make it across the river safely ?
To determine whether Tarzan can safely cross the river using the vine, we need to analyze the forces acting on him at the lowest point of the swing. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on Tarzan
At the lowest point of the swing, two forces act on Tarzan:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The tension in the vine acting upwards, which we will denote as T.
Step 2: Calculate the Gravitational Force
The gravitational force can be calculated using the formula:
Fg=mg
Where:
- m=85.0kg (mass of Tarzan)
- g=9.81m/s2 (acceleration due to gravity)
Calculating Fg:
Fg=85.0kg×9.81m/s2=850N
Step 3: Calculate the Centripetal Force
At the lowest point of the swing, Tarzan also experiences centripetal acceleration due to his circular motion. The centripetal force is given by:
Fc=mv2r
Where:
- v=8.00m/s (speed at the bottom of the swing)
- r=10.0m (length of the vine)
Calculating Fc:
Fc=85.0kg×(8.00m/s)210.0m=85.0×6410=544N
Step 4: Calculate the Total Tension in the Vine
The total tension T in the vine at the lowest point is the sum of the gravitational force and the centripetal force:
T=Fg+Fc
Substituting the values:
T=850N+544N=1394N
Step 5: Compare the Tension with the Breaking Strength of the Vine
The breaking strength of the vine is given as 1000N. We compare the calculated tension with this value:
T=1394N>1000N
Conclusion
Since the tension in the vine exceeds its breaking strength, the vine will break. Therefore, Tarzan will not make it across the river safely.
Final Answer
The vine will break, and Tarzan won't make it past the river safely.
---
At the lowest point of the swing, two forces act on Tarzan:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The tension in the vine acting upwards, which we will denote as T.
The gravitational force can be calculated using the formula:
Fg=mg
Where:
- m=85.0kg (mass of Tarzan)
- g=9.81m/s2 (acceleration due to gravity)
Fg=85.0kg×9.81m/s2=850N
At the lowest point of the swing, Tarzan also experiences centripetal acceleration due to his circular motion. The centripetal force is given by:
Fc=mv2r
Where:
- v=8.00m/s (speed at the bottom of the swing)
- r=10.0m (length of the vine)
Fc=85.0kg×(8.00m/s)210.0m=85.0×6410=544N
The total tension T in the vine at the lowest point is the sum of the gravitational force and the centripetal force:
T=Fg+Fc
Substituting the values:
T=850N+544N=1394N
The breaking strength of the vine is given as 1000N. We compare the calculated tension with this value:
T=1394N>1000N
Since the tension in the vine exceeds its breaking strength, the vine will break. Therefore, Tarzan will not make it across the river safely.
The vine will break, and Tarzan won't make it past the river safely.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 100N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m.ifg =10 ms^(-1), what is the speed of just before it touches the spring?
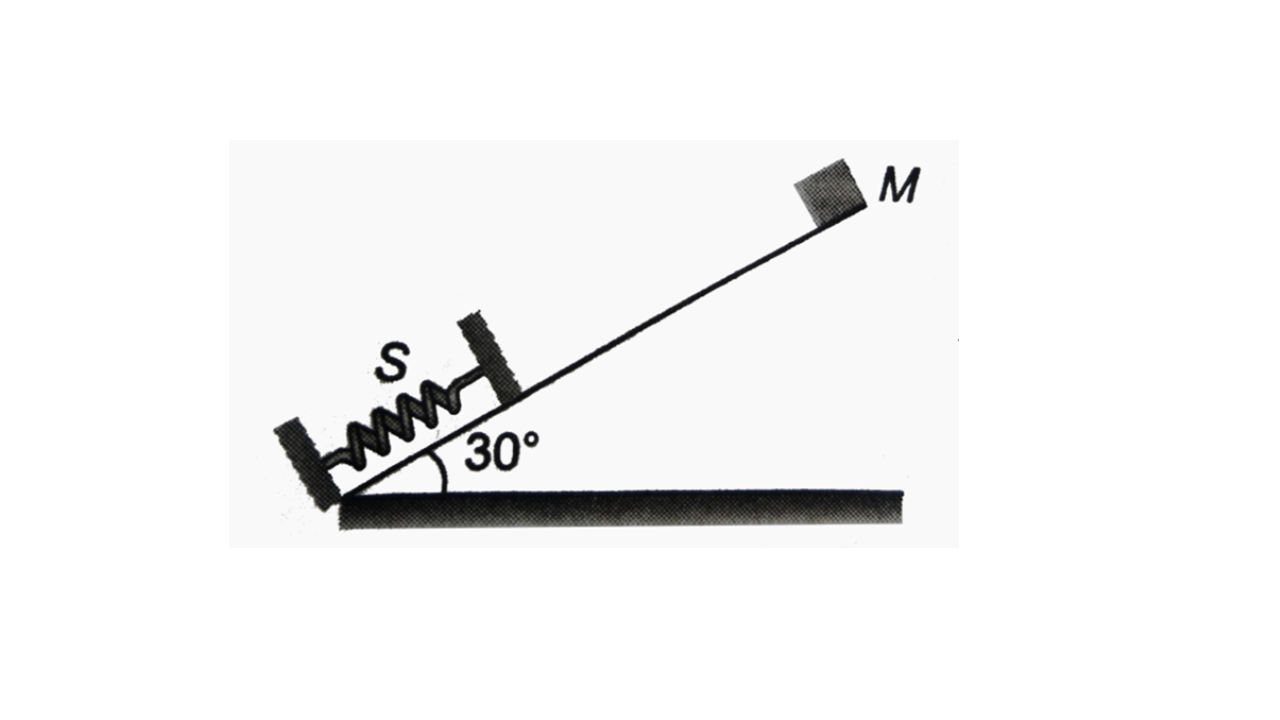 .
.
View SolutionThe speed of a swimmer in still water is 20 m//s. The speed of river water of river water is 10 m//s and due east. If he is standing on the south bank and wishes to cross the river along the shortest path the angle at which he should make his stroke w.r.t. noth is given by :-
View Solution
Knowledge Check
The mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of 10ms−1. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take g=10ms−2.
A300NB600NC1200ND150N
An air bubble of radius 2.0mm is formed at the bottom of a 3.3m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure =1.0×105Pa and desnity of water=1000kg m^(-3).
View SolutionA man can swim with a speed of 4kmh−1 in still water. He crosses a river 1km wide that flows steadly at 3kmh−1. If he makes his strokes normal to the river current, how far down the river does he go when he reaches the other bank?
View SolutionA river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionA swimmer is capable of swimming at 1.65ms- in still water. If he swims directly across a 180m wide river with water flow at 0.85ms−1', how far down stream will he reach? How long will it take to reach the other side ?
View Solutiona. Estimate the force with which a karate master strikes a board, assuming that hand's speed at the moment of impact is 10.0ms−1, decreasing to 1.00ms−1 during a 0.002s time interval of contact between the hand and the board. The mass of his hand and arm is 1.00kg .
b Estimate the shear, assuming this force it exerted on a 1.00cm thick pine board that is 10.0cm wide.
c. If we maximum shear stress a pine board can support before breaking is 3.60×106N/m2, will the board break?
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00. What should be the initial downward speed of the rocketeer so that he catches the student at the top of 100 the floor for safe landing ?
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
In Q.1, what would be the approximate retardation to be given by jet pack along for safe landing?
View Solution
