Ten one-rupee coins are put on top each other on a table. Each coin has a mass m. The rection of the 6th coin (counted from the bottom) on the 7th coin is
4mg
6mg
7mg
3mg
The correct Answer is:A
To solve the problem of finding the reaction force of the 6th coin on the 7th coin in a stack of 10 one-rupee coins, each with mass m, we can follow these steps:
1. Identify the Coins and Their Arrangement:
- We have a total of 10 coins stacked on top of each other.
- Each coin has a mass m.
- We need to focus on the 6th coin (from the bottom) and its reaction force on the 7th coin.
2. Determine the Mass Above the 6th Coin:
- The 6th coin is at the bottom of the top 4 coins (7th, 8th, 9th, and 10th).
- Therefore, the total mass of the coins above the 6th coin is 4m (since there are 4 coins above it).
3. Draw the Free Body Diagram (FBD):
- In the FBD of the 6th coin, we have:
- The weight of the 4 coins above it acting downwards, which is 4mg.
- The reaction force R exerted by the 6th coin on the 7th coin acting upwards.
4. Apply Newton's Second Law:
- Since the system is in equilibrium (the coins are at rest), the sum of forces acting on the 6th coin must be zero.
- Therefore, we can set up the equation:
R−4mg=0
- Rearranging gives:
R=4mg
5. Conclusion:
- The reaction force of the 6th coin on the 7th coin is R=4mg.
Final Answer:
The reaction of the 6th coin on the 7th coin is 4mg.
---
- We have a total of 10 coins stacked on top of each other.
- Each coin has a mass m.
- We need to focus on the 6th coin (from the bottom) and its reaction force on the 7th coin.
- The 6th coin is at the bottom of the top 4 coins (7th, 8th, 9th, and 10th).
- Therefore, the total mass of the coins above the 6th coin is 4m (since there are 4 coins above it).
- In the FBD of the 6th coin, we have:
- The weight of the 4 coins above it acting downwards, which is 4mg.
- The reaction force R exerted by the 6th coin on the 7th coin acting upwards.
- Since the system is in equilibrium (the coins are at rest), the sum of forces acting on the 6th coin must be zero.
- Therefore, we can set up the equation:
R−4mg=0
- Rearranging gives:
R=4mg
- The reaction force of the 6th coin on the 7th coin is R=4mg.
The reaction of the 6th coin on the 7th coin is 4mg.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Ten one-rupee coins are put on top of each other on a table, Each coin has a mass m. Which of the following statements in not ture?
View SolutionTen coins are arranged one above the other. The mass of each coin is 10 g. Reaction force of the sixth coin from the bottom of the seventh coin is
View Solution
Knowledge Check
If 50 one-cent coins were stacked on top of each other in a column, the column would be approximately 378 inches tall. At this rate, which of the following is closest to the number of one-cent coins it would take to make an 8-inch-tall column?
A75B100C200D390
Ten coins each of mass 10 gm are placed one above the other. The reaction force exerted by 7th coin from the bottom on the 8th coin is (g=10ms−2)
(a) 0.3 N
(b) 0.2 N
(c) 0.4 N
(d) 0.7 N
View SolutionThere are two temples, one on each bank of a river, just opposite to each other. One temple is 50m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30o and 60o respectively. Find the width of the river and the height of the other temple.
View SolutionFind the probability of drawing a one-rupee coin from a purse with two compartments one of which contains 3 fifty-paise coins and 2 one-rupee coins and other contains 2 fifty-paise coins and 3 one-rupee coins.
View SolutionA bag contains four one-rupee coins, two twenty-five paisa coins, and five ten-paisa coins. In how many ways can an amount, not less than Rs. 1 be taken out from the bag? (Consider coins of the same denominations to be identical.) a. 71 b. 72 c. 73 d. 80
View SolutionA purse contains 3 silver and 6 copper coins a second purse contains 4 silver and 3 copper coins.If a coin is drawn at random from one of the two purses,find the probability that it is a silver coin.
View SolutionA man wants to distribute 101 coins a rupee each, among his 3 sons with the condition that no one receives more money than the combined total of other two. The number of ways of doing this is :-
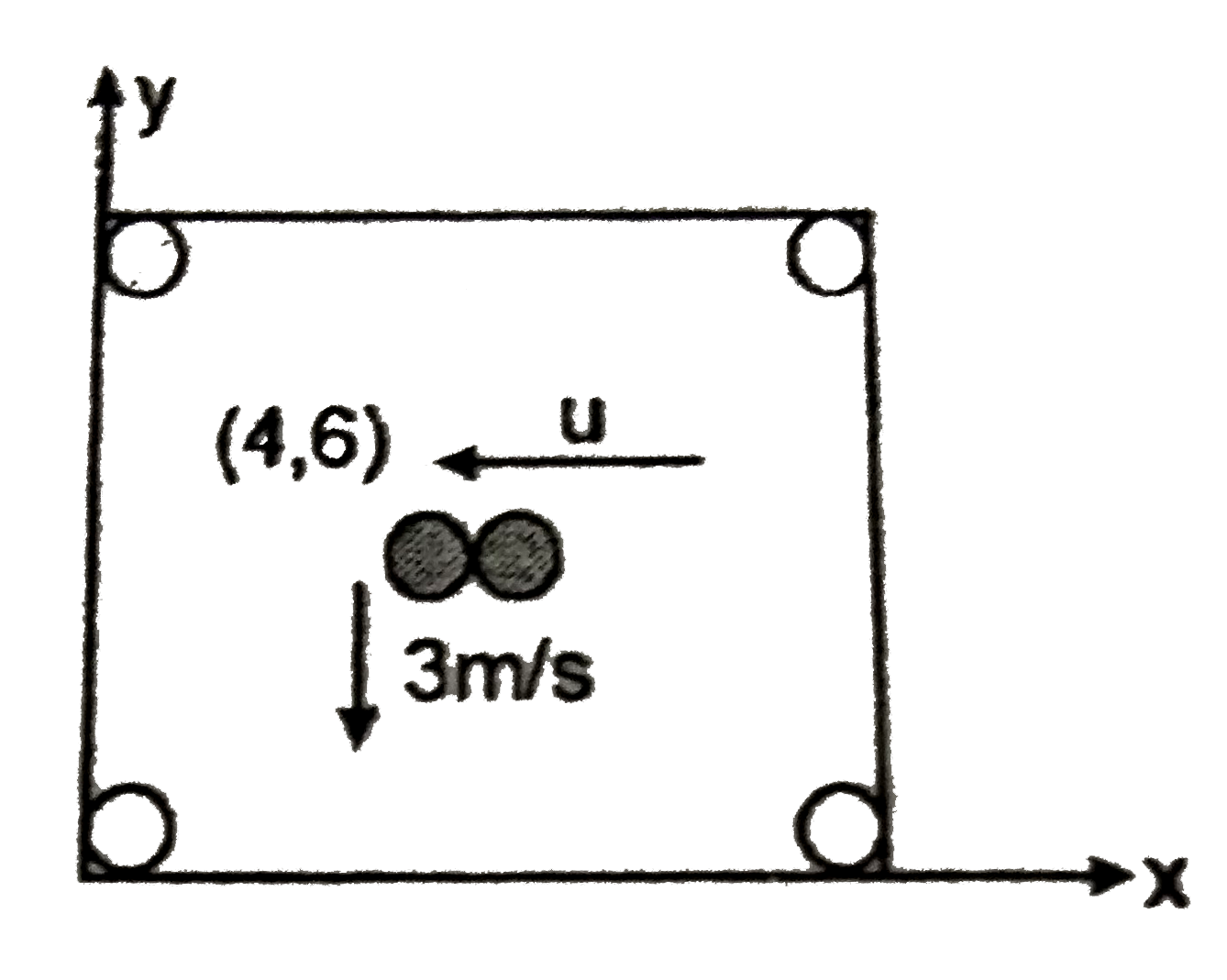
View SolutionOn a smooth carrom board. A coin located at (4,6) is moving in negative y−direction with speed 3m/s is being hit at that point by a striker moving along negative x− axis . The line joining centre of the coin and striker just before the collision is parallel to x− axis. After collision the coin goes into the hole located at origin. Mass of the striker and the coin is equal. Considering the collision to be elastic, find the velocity ( in vector form ) of the stricker before the collision and after the collision.
View Solution
