Tension applied to a wire of length 1m and its mass 1g, if it is to vibrate with the fundamental frequency of 50 Hz, will be
100N
10N
50N
2.5N
The correct Answer is:B
m=m'l=10−31∴n=12l√Tm
∴T=4l2n2m=4×1×2500×10−3=10N
Topper's Solved these Questions
Similar Questions
Discuss different modes of vibrations in an air column of a pipe open at both the ends. State the cause of end correction. Find the end correction for the pipe open at both the ends in fundamental mode.
What should be tension applied to a wire of length 1m and maas 10 g, if it has to vibrate with fundamental frequency of 50 Hz?
View SolutionA string vibrating with a fundamental frequency of 8 Hz has tension T1. This string vibrates with a fundamental frequency of 15 Hz when the tension is T2 .
Find the fundamental frequency of the string when its tension is T1+T2 .
View Solution
Knowledge Check
What tension should be there in a string of length 0.8m and of mass 5×10−3kg, if it vibrates with fundamental frequency of 100 Hz?
A100NB160NC140ND120NA wire is under a tension of 32N and length between the two bridges in 1m. If the length of the sample wire is 10m and its mass is 2 g, then the fundamental frequency of the wire will be
A400HzB200HzC100HzD800HzA piano wire has a length of 81 cm and a mass of 2.0 g. If its fundamental frequency is to be 394 Hz, it tension must be
A0.32 NB63 NC130 ND250 N
A metallic wire with tension T and at temperature 30∘C vibrates with its fundamental frequency of 1kHz. The same wire with the same tension but at 10∘C temperature vibrates with a fundamental frequency of 1.001kHz. The coefficient of linear expansion of the wire is equal to 10−K.∘C. Find 2K.
View SolutionA wire is under tension and emitting its fundamental frequency . If the wire is replaced by another wire of the same material and same tension but it is thicker , then the fundamental frequency of vibration will
View SolutionTwo identical wires of length land2l vibrate with fundamental frequencies 100 Hz and 150 Hz respectively. What is the ration of their tensions?
View SolutionIn law of tension, the fundamental frequency of vibrating string is
View SolutionIn a sonometer wire, the tension is maintained by suspending a 20kg mass from the free end of the wire. The fundamental frequency of vibration is 300Hz.
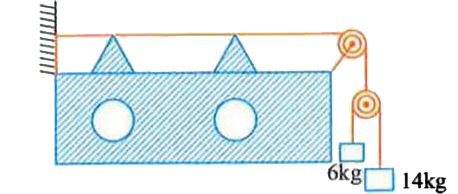
If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as show in the figure the fundamental frequency will
View Solution
