Question

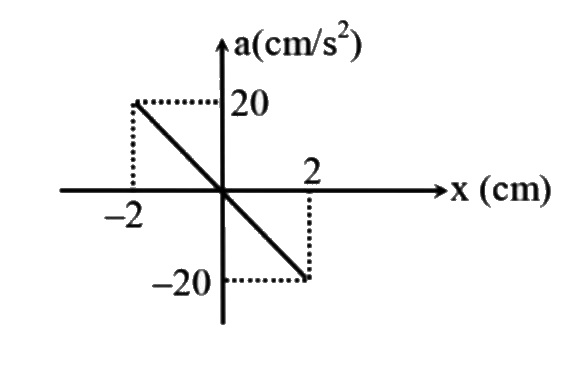
The acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is

Options

A. `(4 pi)/(sqrt(3))s`
B. `(2 pi)/(sqrt(3))s`
C. The given graph doesn't represent simple harmonic motion
D. information is insufficient

Answer

A

Explanation

To find the time period of a particle executing simple harmonic motion (SHM) from the acceleration-displacement graph, we can follow these steps:

1. Understand the Relationship:
In SHM, the acceleration \( a \) is related to the displacement \( x \) by the equation:
\( a = -\omega^2 x \)
This indicates that the acceleration is directly proportional to the displacement but in the opposite direction.

2. Identify the Graph Type:
The graph of acceleration versus displacement is a straight line with a negative slope. This can be expressed in the form \( y = mx + c \), where \( y \) is acceleration \( a \) and \( x \) is displacement \( x \).

3. Determine the Slope:
The slope of the line \( m \) can be defined as:
\( m = \frac{dy}{dx} \)
Since the graph shows a negative slope, we can denote it as:
\( m = -\omega^2 \)

4. Calculate the Slope from the Graph:
If the angle \( \theta \) made with the horizontal is given (for example, \( 37^\circ \)), we can find the slope using:
\( m = -\tan(\theta) \)
For \( \theta = 37^\circ \):
\( \tan(37^\circ) = \frac{3}{4} \)
Therefore, the slope \( m \) becomes:
\( m = -\frac{3}{4} \)

5. Relate the Slope to Angular Frequency:
From the relationship \( m = -\omega^2 \), we have:
\( -\omega^2 = -\frac{3}{4} \)
Thus, we can write:
\( \omega^2 = \frac{3}{4} \)

6. Find Angular Frequency:
Taking the square root gives:
\( \omega = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2} \)

7. Relate Angular Frequency to Time Period:
The angular frequency \( \omega \) is related to the time period \( T \) by the equation:
\( \omega = \frac{2\pi}{T} \)
Therefore, we can rearrange this to find \( T \):
\( T = \frac{2\pi}{\omega} \)

8. Substitute the Value of \( \omega \):
Substituting \( \omega = \frac{\sqrt{3}}{2} \):
\( T = \frac{2\pi}{\frac{\sqrt{3}}{2}} = \frac{4\pi}{\sqrt{3}} \)

9. Final Answer:
The time period of the simple harmonic motion is:
\( T = \frac{4\pi}{\sqrt{3}} \)