The air if filled in a balloon and the volume of balloon increases gradually. Find the rate of increase of volume of balloon with radius when of balloon becomes 30 cm.

Video Solution

Text Solution

Verified by Experts

Here radius of balloon r = 30 cm
Volume of balloon, $V = \frac{4}{3} π r^{3}$
Rate of increase of volume of balloom w.r.t radius
$\frac{d V}{d t} = \frac{d}{d r} (\frac{4}{3} π r^{3}) = \frac{4}{3} π \times 3 r^{2} = 4 π r^{2}$
When r =30 cm = 0.30m
$\frac{d V}{d r} = 4 \times \frac{22}{7} \times {(0.30)}^{2} = 1.13 m^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Which gas is filled in the balloon?
AHydrogen
BCarbon dioxide
CHelium
DOxygen
Question 2 - Select One
A balloon is pumped at the rate of $a$ $c m^{3}$ /minute. The rate of increase of its surface area when the radius is $b$ $c m$ , is
A $\frac{2 a^{2}}{b^{4}} c m^{2} / min$
B $\frac{a}{2} b c m^{2}$ /min
C $\frac{2 a}{b} c m^{3}$ /min
DNone of these
Question 3 - Select One
A conducting bolloon of the radius a is charged to potential $V_{0}$ and held at a large height above the earth ensures that charge distribution on the surface of the balloon remains unaffected by the presence of the earth. It is connected to the earth through a resistance R and a value in the balloon is opened . The gas inside the balloon escapes from value and the size of the balloon decreases. The rate of decrease in radius of the balloon is controlled in such a manner that potential of the balloon remains constant. Assume the electric permittivity of the surrounding air equals to that of free space $(ε_{0})$ and charge cannot leak to the surrounding air.

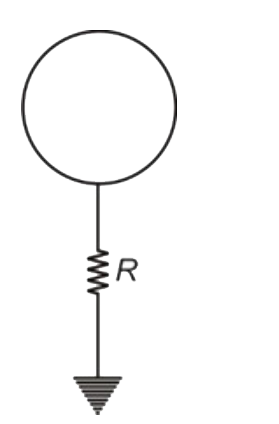
The rate at which radius r of the balloon changes with time is best represented by the equation
A $\frac{d r}{d t} = \frac{1}{4 π ε_{0} R}$
B $\frac{d r}{d t} = - \frac{1}{4 π ε_{0} R}$
C $\frac{d r}{d t} = \frac{1}{4 π ε_{0} a R}$
D $\frac{d r}{d t} = - \frac{r}{4 π ε_{0} a R}$

PRADEEP-MATHEMATICAL TOOLS-Fill in the blanks

Home
Ask Doubt
Profile